El área bajo una curva puede ser encontrada usando integrales definidas. A su vez, las integrales definidas son calculadas al integrar la función y evaluar tanto al límite inferior, como al límite superior. El límite inferior es restado del límite superior para obtener un valor determinado para el área.
A continuación, veremos 8 ejercicios resueltos del área bajo una curva. Además, veremos algunos ejercicios prácticos para aplicar lo aprendido.
Proceso usado para encontrar el área bajo una curva
Consideramos el área $latex A$ bajo la curva $latex f(x)$ que se muestra en el siguiente diagrama:
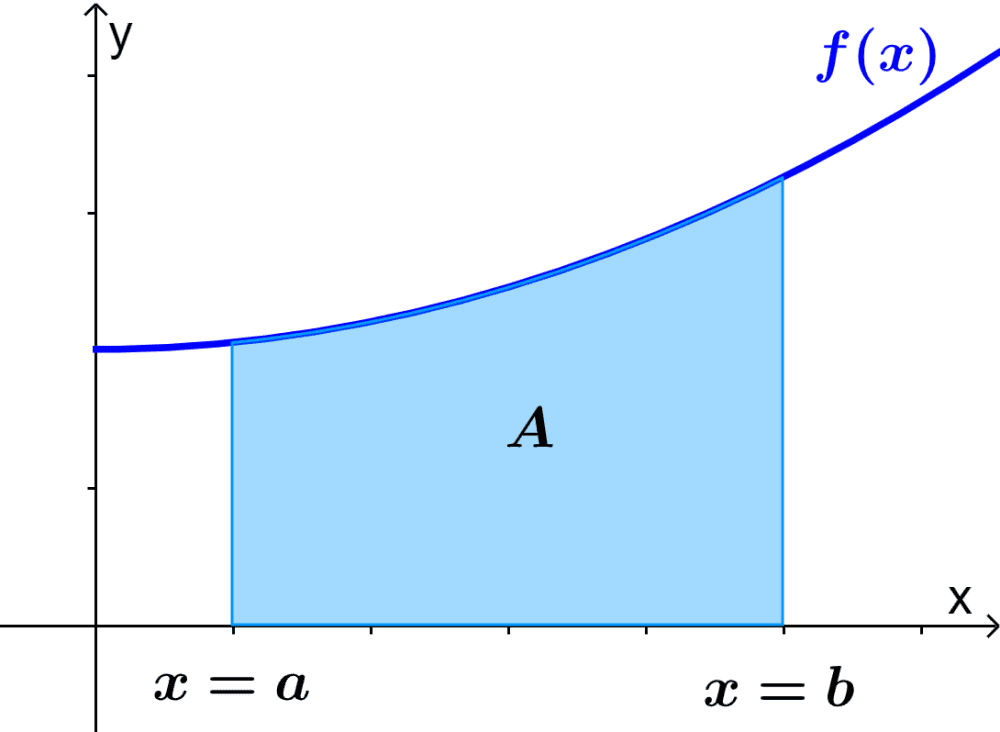
Podemos encontrar el área bajo esta curva usando una integral definida. En este caso, el área bajo la curva está representada por $latex A= \int_{a}^{b} f(x)dx$, en donde,
- $latex dx$ indica que los límites $latex a $ y $latex b$ son límites de x.
- La constante $latex a$ es el límite inferior de la integral.
- La constante $latex b$ es el límite superior de la integral.
Tomando esto en cuenta, podemos seguir los siguientes pasos para encontrar el área bajo una curva suponiendo que queremos encontrar el área bajo $latex 2x$ entre $latex x=0$ y $latex x=1$.
Paso 1: Formar una integral definida con la información dada. En este caso, tenemos la siguiente integral:
$latex \int_{0}^{1} 2xdx$
Paso 2: Obtener la integral de la función y expresarla usando corchetes, en donde escribimos a los límites de integración de la siguiente forma:
$latex \int_{0}^{1} 2xdx=[x^2+c]_{0}^{1}$
Paso 3: Evaluamos los límites superior e inferior en la expresión integrada. Restamos el límite inferior del límite superior:
$latex [x^2+c]_{0}^{1}=[(1)^2+c]-[(0)^2+c]$
Paso 4: Simplificar hasta obtener un único valor numérico:
$latex =[(1)^2+c]-[(0)^2+c]$
$latex =[1+c]-[0+c]$
$latex =1$
El valor encontrando corresponde al área.
Cuando resolvemos integrales definidas, generalmente las constantes de integración son ignoradas, ya que serán canceladas en el paso 3 de todas formas.
Ejercicios resueltos del área bajo una curva
EJERCICIO 1
¿Cuál es el área bajo la curva representada por $latex y=x^2$ entre $latex x=1$ y $latex x=3$?
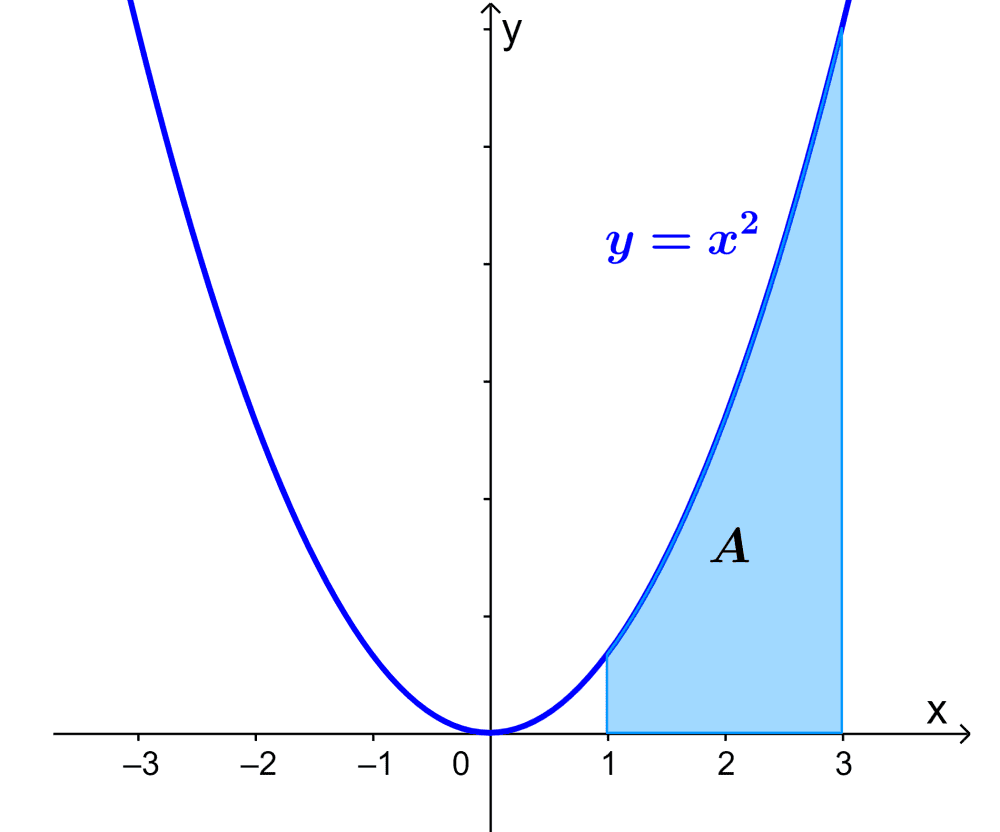
Solución
Para resolver este ejercicio, tenemos que empezar formando una integral definida con la información dada. Entonces, tenemos:
$$A=\int_{1}^{3} x^2 dx$$
Ahora, encontramos la integral de la expresión y mantenemos los límites de integración usando corchetes:
$$A=\left[ \frac{x^3}{3} \right]_{1}^{3}$$
Cuando evaluamos los límites de integración, tenemos:
$$A=\left[ \frac{(3)^3}{3} \right]-\left[ \frac{(1)^3}{3} \right]$$
Finalmente, podemos simplificar:
$$A=\left[ \frac{27}{3} \right]-\left[ \frac{1}{3} \right]$$
$$A=[9]-\left[ \frac{1}{3} \right]$$
$$A= \frac{26}{3}$$
EJERCICIO 2
Determina el área bajo la curva que es representada por $latex y=\frac{1}{3}x^2+2$ desde $latex x=0$ y $latex x=3$.
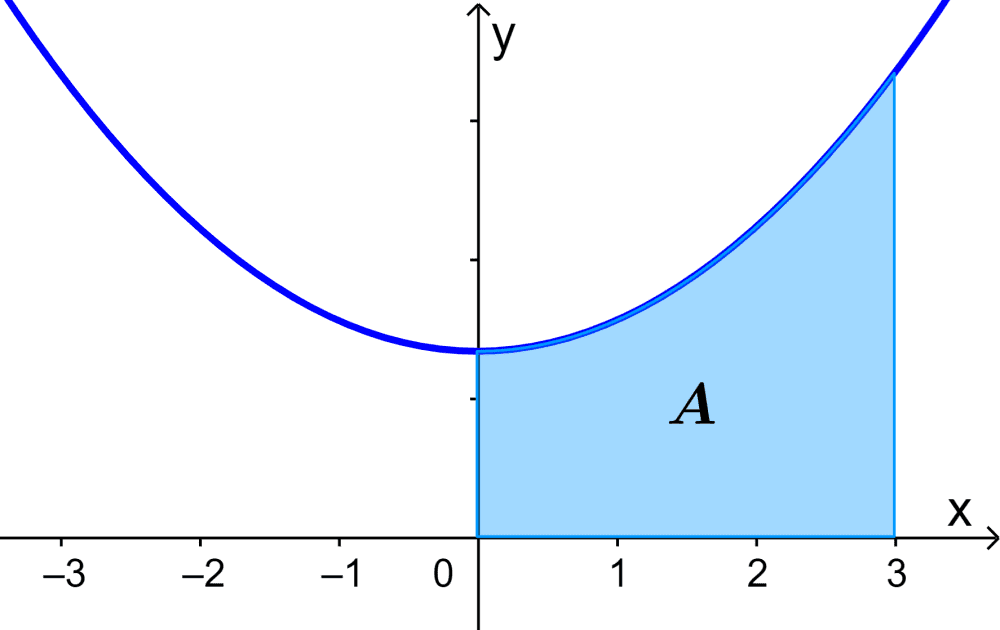
Solución
Con la información dada, podemos formar la siguiente integral definida:
$$A=\int_{0}^{3} \frac{1}{3} x^2+2 dx$$
Ahora, integramos a la expresión dada y mantenemos los límites de integración:
$$A=\left[ \frac{1}{9} x^3+2x \right]_{0}^{3}$$
Cuando evaluamos los límites de integración en la expresión integrada, tenemos:
$$A=\left[\frac{1}{9}(3)^3+2(3) \right]-\left[\frac{1}{9}(0)^3+2(0) \right]$$
Al simplificar, tenemos:
$$A=[3+6]-[0]$$
$$A=9$$
EJERCICIO 3
¿Cuál es el área de la curva representada por $latex y=x^3-4x$ desde $latex x=-2$ hasta $latex x=0$?
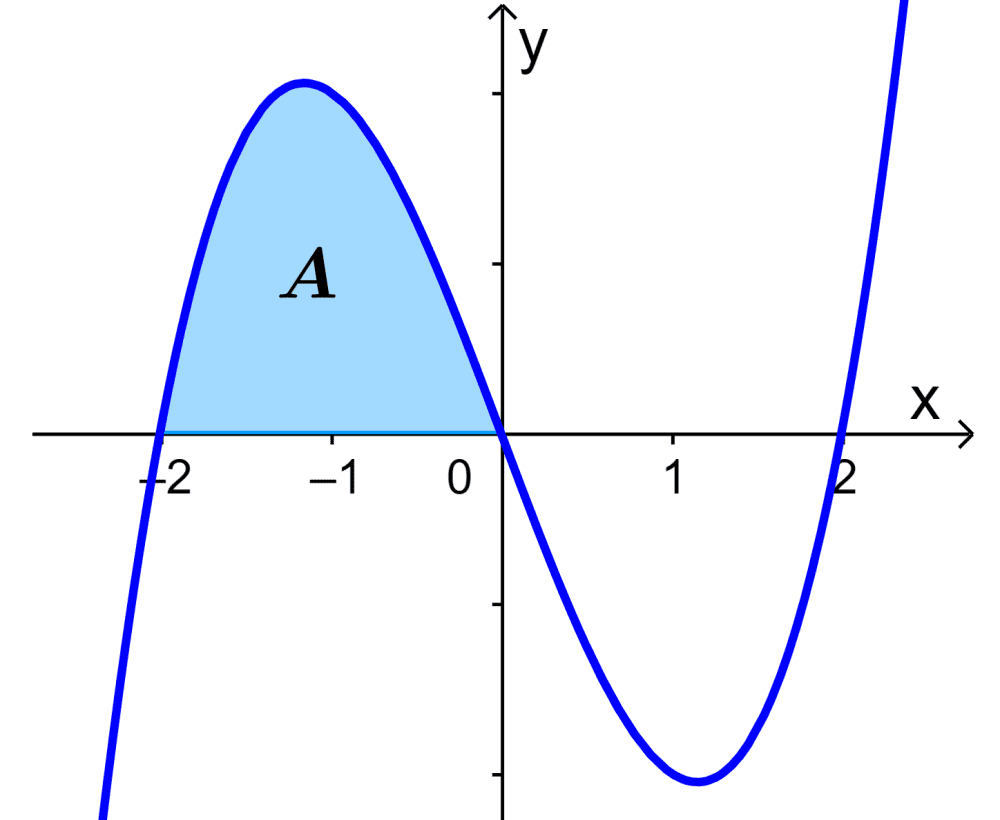
Solución
Empezamos formando una integral definida con la información dada:
$$A=\int_{-2}^{0} x^3-4x dx$$
Ahora, integramos la expresión y mantenemos los límites de integración:
$$A=\left[ \frac{x^4}{4} -2x^2 \right]_{-2}^{0}$$
Cuando evaluamos los límites de integración, tenemos:
$$A=\left[ \frac{(0)^4}{4} -2(0)^2 \right]-\left[ \frac{(-2)^4}{4} -2(-2)^2 \right]$$
Simplificamos para obtener un solo valor para el área:
$$A=[ 0 -0]-\left[ \frac{16}{4} -2(4) \right]$$
$latex A=-[ 4-8]$
$latex A= 4$
EJERCICIO 4
Encuentra el área bajo la curva $latex y=x^2+x+2$ desde $latex x=-1$ hasta $latex x=2$.
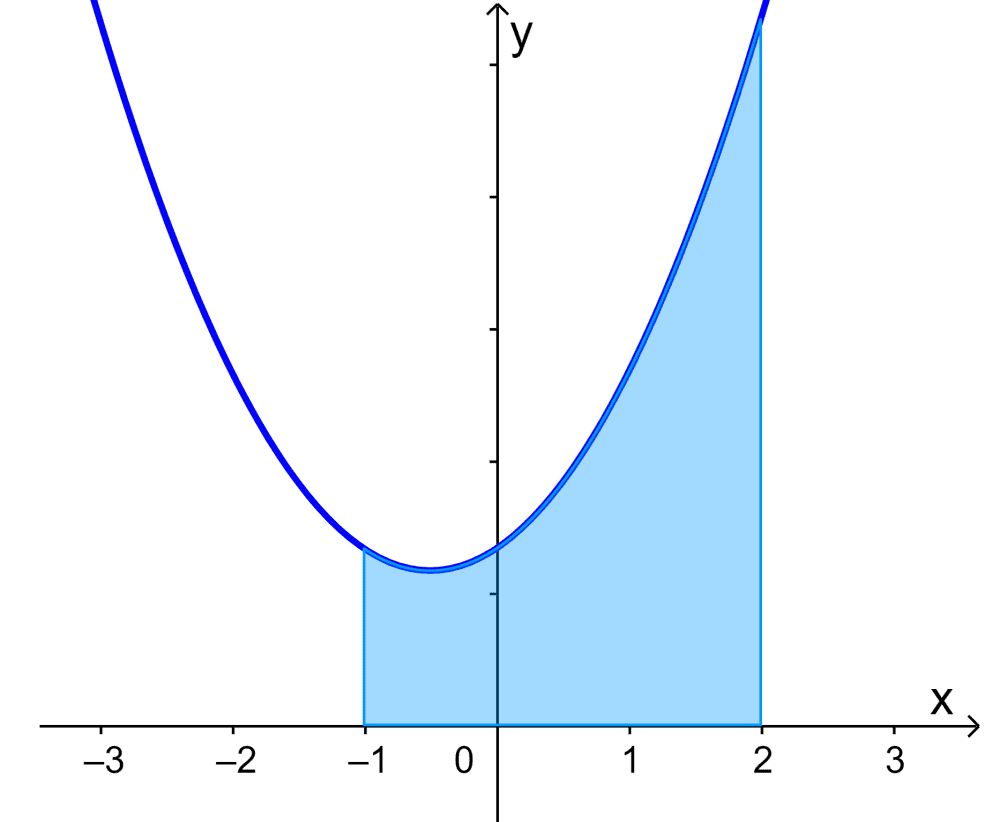
Solución
Formando una integral con la información dada, tenemos:
$$A=\int_{-1}^{2} x^2+x+2 dx$$
Ahora, podemos integrar la expresión mientras mantenemos los límites de integración:
$$A=\left[ \frac{x^3}{3} +\frac{x^2}{2}+2x \right]_{-1}^{2}$$
Al evaluar esto, tenemos:
$$A=\left[ \frac{(2)^3}{3} +\frac{(2)^2}{2}+2(2) \right]-\left[ \frac{(-1)^3}{3} +\frac{(-1)^2}{2}+2(-1) \right]$$
Cuando simplificamos, tenemos:
$$A=\left[ \frac{8}{3} +2+4 \right]-\left[ -\frac{1}{3} +\frac{1}{2}-2 \right]$$
$$A=\left[ \frac{26}{3}\right]-\left[ -\frac{11}{6} \right]$$
$latex A=\frac{63}{6}$
$latex A= 10~\frac{1}{2}$
EJERCICIO 5
Si es que tenemos una curva representada por $latex y=x^2+4x$, encuentra el área de la región que va desde $latex x=-2$ hasta $latex x=0$.
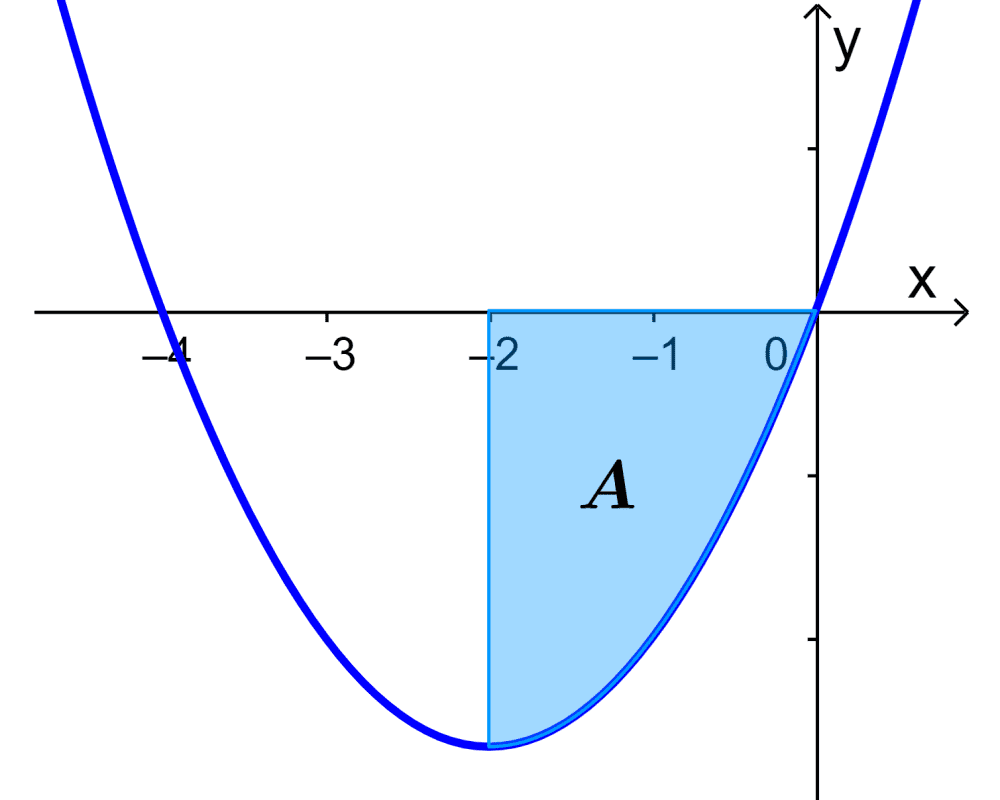
Solución
En este caso, la región que queremos está debajo del eje x. Sin embargo, podemos seguir el mismo proceso y encontrar una integral definida con la información dada:
$$A=\int_{-2}^{0} x^2 +4x dx$$
Determinando la integral de la expresión y manteniendo los límites de integración, tenemos:
$$A=\left[ \frac{x^3}{3} +2x^2 \right]_{-2}^{0}$$
Al evaluar los límites de integración, tenemos:
$$A=\left[ \frac{(0)^3}{3} +2(0)^2 \right]-\left[ \frac{(-2)^3}{3} +2(-2)^2 \right]$$
Cuando simplificamos, obtenemos lo siguiente:
$$A=[ 0 +0]-\left[ \frac{-8}{3} +8 \right]$$
$$A=-\left[ \frac{16}{3} \right]$$
Vemos que obtuvimos un valor negativo. La razón para esto es que el área que queremos está bajo el eje x. Entonces, ignoramos el signo menos y el área es igual a $latex A= \frac{16}{3} $.
En este ejercicio, podemos entender por qué es útil trazar una gráfica simple cuando queremos encontrar el área bajo una curva.
EJERCICIO 6
Encuentra el área bajo la curva $latex y=3x^2-3x-6$ desde $latex x=-1$ hasta $latex x=2$.
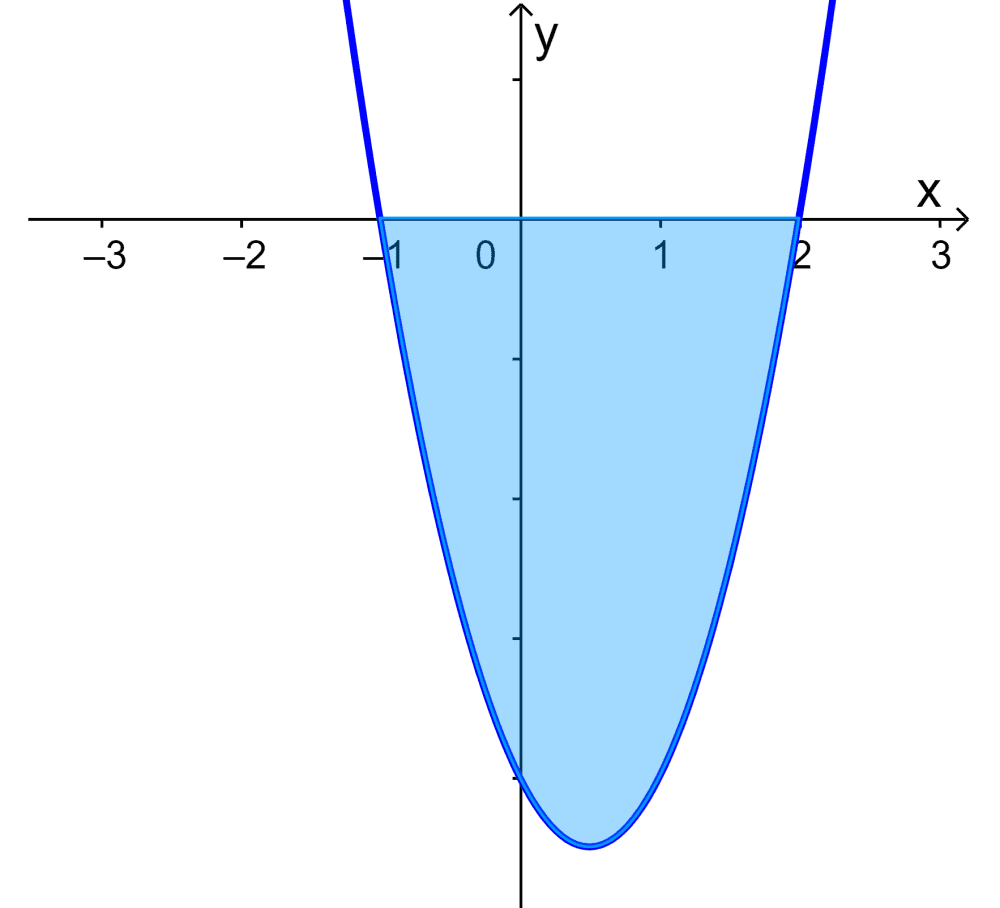
Solución
Este ejercicio es similar al anterior. Entonces, debemos usar el mismo proceso e ignorar el signo negativo resultante.
Formando la integral definida, tenemos:
$$A=\int_{-1}^{2} 3x^2-3x-6 dx$$
Determinando la integral de la expresión y manteniendo los límites de integración, tenemos:
$$A=\left[ x^3 -\frac{3x^2}{2}-6x \right]_{-1}^{2}$$
Cuando evaluamos los límites de integración, tenemos:
$$A=\left[ (2)^3 -\frac{3(2)^2}{2}-6(2) \right]-\left[ (-1)^3 -\frac{3(-1)^2}{2}-6(-1) \right]$$
Al simplificar, tenemos:
$$A=[ 8 -6-12 ]-\left[ -1 -\frac{3}{2}+6 \right]$$
$$A=[ -10 ]-\left[ \frac{7}{2} \right]$$
$$A=-\frac{27}{2}=-13.5$$
El área es igual a $latex A= 13.5 $.
EJERCICIO 7
Encuentra el área bajo la curva $latex y=2x^3-8x$ desde $latex x=-2$ hasta $latex x=2$.
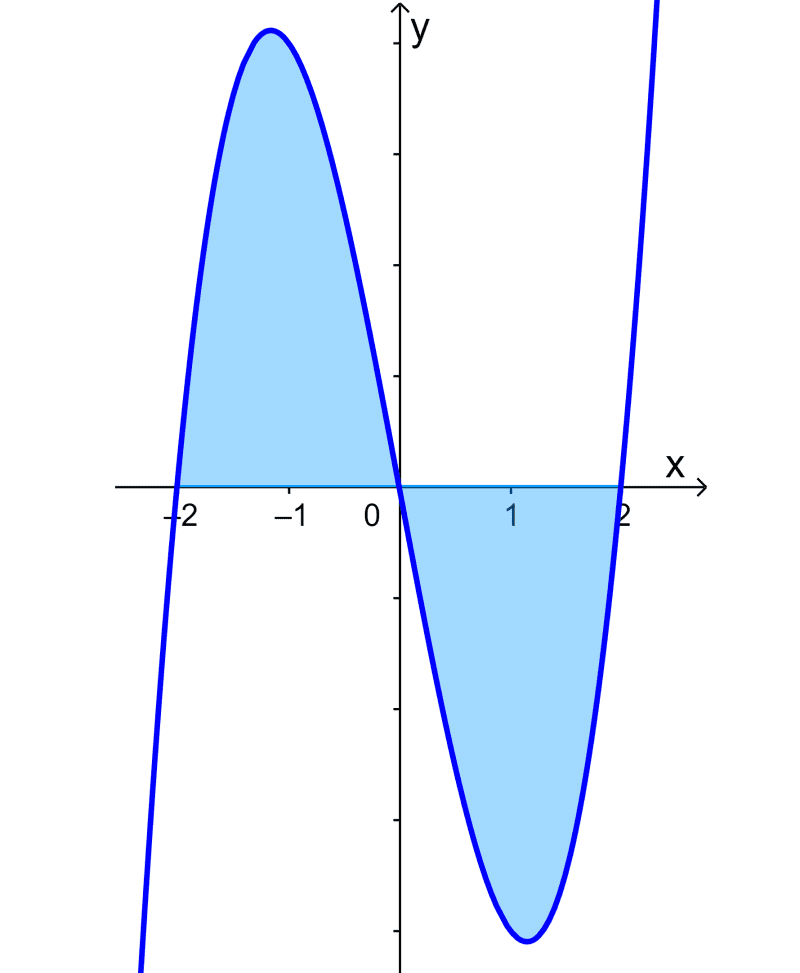
Solución
Podemos resolver esto al encontrar las áreas bajo el eje x y encima del eje x separadamente. Sin embargo, en este caso, observamos que la gráfica es simétrica y ambas regiones tienen la misma área.
Por lo tanto, podemos encontrar el área de una región y luego la multiplicamos por 2. Entonces, empezamos formando la siguiente integral definida:
$$A=\int_{-2}^{0} 2x^3-8x dx$$
Ahora, escribimos de la siguiente forma:
$$A=\left[ \frac{x^4}{2}-4x^2 \right]_{-2}^{0}$$
Al evaluar esto, tenemos:
$$A=\left[ \frac{(0)^4}{2}-4(0)^2 \right]-\left[ \frac{(-2)^4}{2}-4(-2)^2 \right]$$
Finalmente, simplificamos para obtener un solo valor:
$latex A=[0-0]-[ 8 -16]$
$latex A= 8$
Entonces, el área de la región desde $latex x=-2$ hasta $latex x=2$ es 16.
EJERCICIO 8
Si es que tenemos la curva $latex y=x^3-4x^2+3x$, ¿cuál es el área bajo la curva desde $latex x=0$ hasta $latex x=3$?
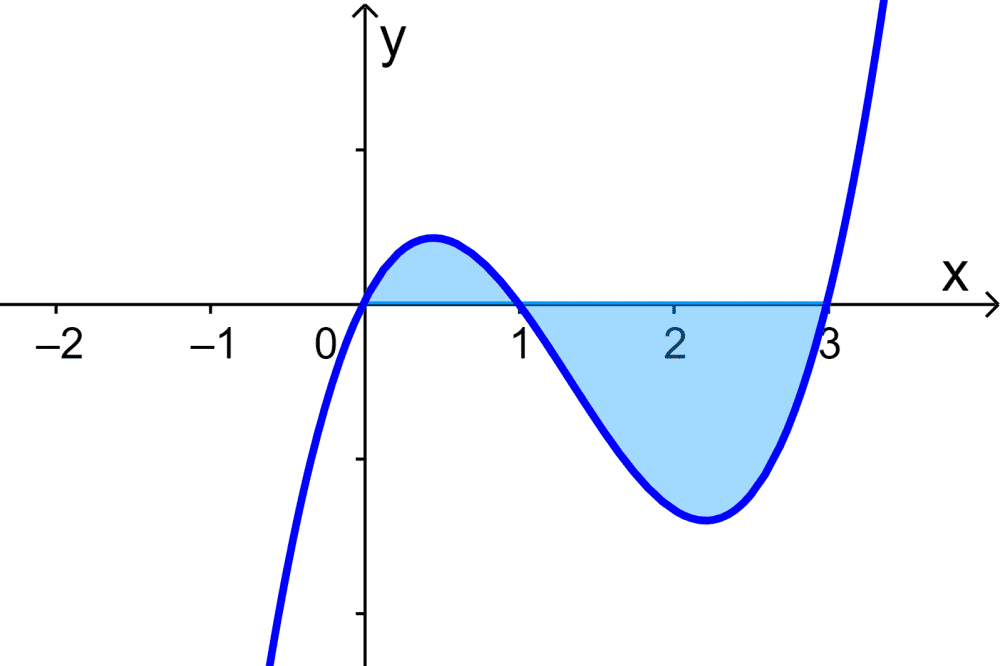
Solución
En este caso, el área requerida tiene dos partes, $latex A_{1}$, el área encima del eje x, y $latex A_{2}$, el área bajo el eje x. Entonces, vamos a encontrar estas áreas separadamente.
Para el área $latex A_{1}$, tenemos la siguiente integral definida:
$$A_{1}=\int_{0}^{1} (x^3-4x^2+3x) dx$$
Podemos resolver esta integral de la siguiente forma:
$$A_{1}=\left[ \frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2} \right]_{0}^{1}$$
$$A_{1}=\left[ \frac{1}{4}-\frac{4}{3}+\frac{3}{2} \right]-[ 0]$$
$$A_{1}=\frac{5}{12}$$
Para el área $latex A_{2}$, tenemos la siguiente integral definida:
$$A_{2}=\int_{1}^{3} (x^3-4x^2+3x) dx$$
Y resolvemos de la siguiente forma:
$$A_{2}=\left[ \frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2} \right]_{1}^{3}$$
$$A_{2}=\left[ \frac{81}{4}-36+\frac{27}{2} \right]-\left[ \frac{1}{4}-\frac{4}{3}+\frac{3}{2} \right]$$
$$A_{2}=-\frac{9}{4}-\frac{5}{12}$$
$$A_{2}=-\frac{8}{3}$$
Finalmente, calculamos el área total $latex A$ de la siguiente forma:
$$A=A_{1}+A_{2}$$
$$A=\frac{5}{12}+\frac{8}{3}$$
$$A=\frac{37}{12}$$
Ejercicios del área bajo una curva para resolver


Encuentra el área bajo la curva $latex y=2x^2+3$ desde $latex x=-1$ hasta $latex x=2$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:


