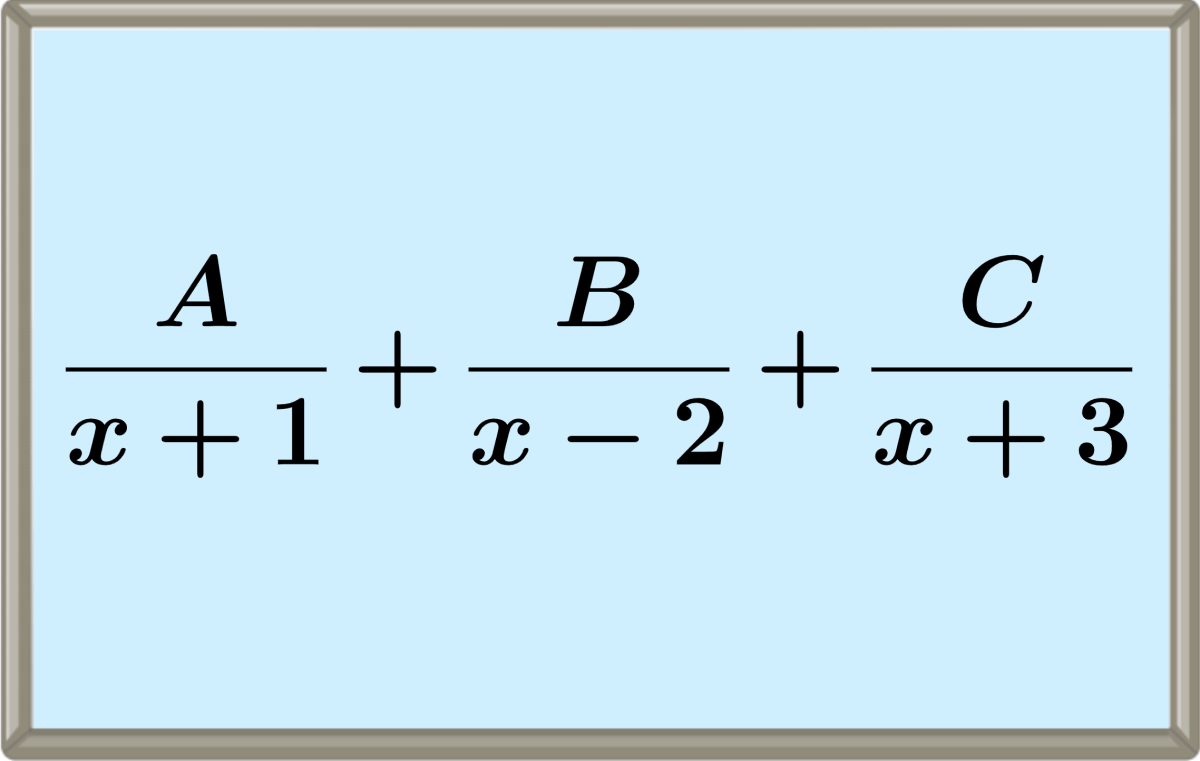Fracciones parciales – Ejercicios resueltos

Esta fracción corresponde al primer caso de fracciones parciales porque tenemos solo factores lineales en su denominador $latex (x+4)$ y $latex (x-3)$.

Entonces, las fracciones parciales de esta fracción tendrán la siguiente forma:

$$\frac{5x+6}{(x+4)(x-3)}=\frac{A}{x+4}+\frac{B}{x-3}$$

Para encontrar los valores de A y B, empezamos multiplicando a toda la expresión por $latex (x+4)(x-3)$ y tenemos:

$$5x+6=A(x-3)+B(x+4)$$

Ahora, podemos sustituir el valor $latex x=3$ para eliminar la constante A y encontrar el valor de B:

$$5(3)+6=A(3-3)+B(3+4)$$

$latex 21=7B$

$latex B=3$

Luego, sustituimos $latex x=-4$ para encontrar el valor de A:

$$5(-4)+6=A(-4-3)+B(-4+4)$$

$latex -14=-7A$

$latex A=2$

Entonces, tenemos

$$\frac{5x+6}{(x+4)(x-3)}=\frac{2}{x+4}+\frac{3}{x-3}$$

El denominador de la fracción tiene dos factores lineales $latex (x+4)$ y $latex (x-6)$. Entonces, su descomposición en fracciones parciales tiene la forma:

$$\frac{7x+8}{(x+4)(x-6)}=\frac{A}{x+4}+\frac{B}{x-6}$$

Cuando multiplicamos a toda la expresión por $latex (x+4)(x-6)$, obtenemos lo siguiente:

$$7x+8=A(x-6)+B(x+4)$$

Ahora, podemos encontrar el valor de B al usar el valor $latex x=6$ para eliminar la constante A:

$$7(6)+8=A(6-6)+B(6+4)$$

$latex 50=10B$

$latex B=5$

Luego, sustituimos $latex x=-4$ para encontrar el valor de A:

$$7(-4)+8=A(-4-6)+B(-4+4)$$

$latex -20=-10A$

$latex A=2$

Entonces, tenemos:

$$\frac{7x+8}{(x+4)(x-6)}=\frac{2}{x+4}+\frac{5}{x-6}$$

A primera vista, la fracción pareciera tener un factor cuadrático en el denominador. Sin embargo, podemos factorizar esta expresión de la siguiente forma:

$$x^2-x-12=(x+3)(x-4)$$

Entonces, la expressión solo tiene factores lineales:

$$\frac{9x^2+34x+14}{(x+2)(x^2-x-12)}=\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}$$

Dado que solo tenemos factores lineales, las fracciones parciales tienen la siguiente forma:

$$\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}=\frac{A}{x+2}+\frac{B}{x+3}+\frac{C}{x-4}$$

Ahora, vamos a multiplicar a toda la expresión por $latex (x+2)(x+3)(x-4)$:

$$ 9x^2+34x+14=A(x+3)(x-4)+B(x+2)(x-4)+C(x+2)(x+3)$$

Podemos encontrar el valor de A al usar $latex x=-2$:

$$ 9(-2)^2+34(-2)+14=A(-2+3)(-2-4)+B(-2+2)(-2-4)+C(-2+2)(-2+3)$$

$latex -18=-6A$

$latex A=3$

Podemos encontrar el valor de B al usar $latex x=-3$:

$$ 9(-3)^2+34(-3)+14=A(-3+3)(-3-4)+B(-3+2)(-3-4)+C(-3+2)(-3+3)$$

$latex -7=7B$

$latex B=-1$

Podemos encontrar el valor de C al usar $latex x=4$:

$$ 9(4)^2+34(4)+14=A(4+3)(4-4)+B(4+2)(4-4)+C(4+2)(4+3)$$

$latex 294=42C$

$latex C=7$

Entonces, las fracciones parciales son:

$$\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}=\frac{3}{x+2}-\frac{1}{x+3}+\frac{7}{x-4}$$

El factor cuadrático $latex (x^2+2)$ del denominador no puede ser factorizado. Entonces, las fracciones parciales tienen la forma:

$$\frac{6x+7}{(x^2+2)(x+3)}=\frac{Ax+B}{x^2+2}+\frac{C}{x+3}$$

Multiplicando a ambos lados de la expresión por $latex (x^2+2)(x+3)$, tenemos:

$$6x+7=(Ax+B)(x+3)+C(x^2+2)$$

Podemos encontrar el valor de C al sustituir $latex x=-3$, de modo que el término $latex (Ax+B)$ sea igual a cero:

$$6(-3)+7=(A(-3)+B)(-3+3)+C((-3)^2+2)$$

$latex -11=11C$

$latex C=-1$

Ahora, podemos encontrar el valor de A al comparar a los coeficientes de los términos con $latex x^2$. En la izquierda no tenemos y en la derecha tenemos $latex Ax^2+Cx^2$. Entonces:

$latex 0=A+C$

Sustituyendo $latex C=-1$ en esta ecuación, obtenemos el valor $latex A=1$.

Podemos encontrar el valor de B al comparar a los coeficientes de los términos constantes:

$latex 7=3B+2C$

Sustituyendo $latex C=-1$ en esta ecuación, obtenemos el valor $latex B=3$.

Entonces, las fracciones parciales son:

$$\frac{6x+7}{(x^2+2)(x+3)}=\frac{x+3}{x^2+2}-\frac{1}{x+3}$$

La expresión cuadrática $latex x^2+3x+5$ en el denominador no puede ser factorizada. Entonces, las fracciones parciales tendrán la siguiente forma:

$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}=\frac{A}{x-6}+\frac{Bx+C}{x^2+3x+5}$$

Para encontrar los valores de A, B y C, empezamos multiplicamos a toda la expresión por $latex (x-6)(x^2+3x+5)$ y tenemos:

$$7x^2+2x-28=A(x^2+3x+5)+(Bx+C)(x-6)$$

Ahora, usamos el valor $latex x=6$ para encontrar el valor de A:

$$7(6)^2+2(6)-28=A((6)^2+3(6)+5)+(B(6)+C)(6-6)$$

$latex 236=59A$

$latex A=4$

Luego, encontramos el valor de B al comparar a los coeficientes de los términos con $latex x^2$:

$latex 7=A+B$

Cuando sustituimos $latex A=4$ en esta ecuación, obtenemos el valor $latex B=3$.

Finalmente, para encontrar el valor de C, comparamos a los términos constantes:

$latex -28=5A-6C$

Cuando sustituimos $latex A=4$ en esta ecuación, obtenemos el valor $latex C=8$.

Entonces, las fracciones parciales son:

$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}=\frac{4}{x-6}+\frac{3x+8}{x^2+3x+5}$$

El denominador de la fracción tiene un factor lineal $latex (x+1)$ y un factor repetido $latex (x+2)^2$. En este caso, las fracciones parciales tienen la siguiente forma:

$$\frac{5x+7}{(x+1)^2(x+2)}=\frac{A}{x+1}+\frac{B}{(x+1)^2}+\frac{C}{x+2}$$

Para encontrar los valores de A, B y C, vamos a multiplicar a toda la expresión por $latex (x+1)^2(x+2)$:

$$5x+7=A(x+1)(x+2)+B(x+2)+C(x+1)^2$$

Al usar el valor $latex x=-1$, tenemos:

$$5(-1)+7=A(-1+1)(-1+2)+B(-1+2)+C(-1+1)^2$$

$latex 2=B$

$latex B=2$

Al usar el valor $latex x=-2$, tenemos:

$$5(-2)+7=A(-2+1)(-2+2)+B(-2+2)+C(-2+1)^2$$

$latex -3=C$

$latex C=-3$

Finalmente, encontramos el valor de A al comparar a los coeficientes con el término $latex x^2$. No tenemos términos en el lado izquierdo y tenemos: $latex Ax^2+Cx^2$ en el derecho:

$latex 0=A+C$

Usando el valor $latex C=-3$ en esta ecuación, encontramos el valor de $latex A=3$. Entonces, tenemos:

$$\frac{5x+7}{(x+1)^2(x+2)}=\frac{3}{x+1}+\frac{2}{(x+1)^2}-\frac{3}{x+2}$$

El denominador de esta fracción tiene un factor lineal $latex (2x+1)$ y un factor repetido $latex (x-2)^2$. Entonces, sus fracciones parciales tienen la siguiente forma:

$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}=\frac{A}{2x+1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}$$

Para encontrar los valores de las constantes, multiplicamos a toda la expresión por $latex (2x+1)(x-2)^2$:

$$2x^2+29x-11=A(x-2)^2+B(2x+1)(x-2)+C(2x+1)$$

Ahora, usamos el valor $latex x=-\frac{1}{2}$ para encontrar el valor de A:

$$2(-\frac{1}{2})^2+29(-\frac{1}{2})-11=A(-\frac{1}{2}-2)^2+B(2(-\frac{1}{2})+1)(-\frac{1}{2}-2)+C(2(-\frac{1}{2})+1)$$

$$-25=\frac{25}{4}A$$

$latex A=-4$

Luego, usamos el valor $latex x=2$ para encontrar el valor de C:

$$2(2)^2+29(2)-11=A(2-2)^2+B(2(2)+1)(2-2)+C(2(2)+1)$$

$latex 55=5C$

$latex C=11$

Si es que comparamos los coeficientes de los términos con $latex x^2$, tenemos:

$latex 2=A+2B$

Sustituyendo $latex A=-4$ en esta ecuación, encontramos el valor de $latex B=3$. Entonces, tenemos:

$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}=-\frac{4}{2x+1}+\frac{3}{x-2}+\frac{11}{(x-2)^2}$$

Podemos observar que el grado del polinomio del numerador es igual a 2 y el grado del denominador también es igual a 2.

En este caso, tenemos una fracción impropia y sus fracciones parciales tienen la siguiente forma:

$$\frac{5x^2-71}{(x+5)(x-4)}=A+\frac{B}{x+5}+\frac{C}{x-4}$$

Ahora, vamos a multiplicar a toda la expresión por $latex (x+5)(x-4)$ y tenemos:

$$5x^2-71=A(x+5)(x-4)+B(x-4)+C(x+5)$$

Luego, vamos a encontrar el valor de A al comparar a los coeficientes de los términos con $latex x^2$ y encontramos que $latex A=5$.

Podemos encontrar el valor de B al sustituir $latex x=-5$ en la expresión:

$$5(-5)^2-71=B(-5-4)$$

$latex 54=-9B$

$latex B=-6$

Podemos encontrar el valor de C al sustituir $latex x=4$ en la expresión:

$$5(4)^2-71=C(4+5)$$

$latex 9=9C$

$latex C=1$

Entonces, tenemos:

$$\frac{5x^2-71}{(x+5)(x-4)}=5-\frac{6}{x+5}+\frac{1}{x-4}$$

Este ejercicio es similar al anterior porque el los polinomios del numerador y del denominador tienen el mismo grado. Entonces, tenemos:

$$\frac{2x^2+x-5}{(x+2)(x+1)}=A+\frac{B}{x+2}+\frac{C}{x+1}$$

Ahora, vamos a multiplicar a toda la expresión por $latex (x+2)(x+1)$ y tenemos:

$$2x^2+x-5=A(x+2)(x+1)+B(x+1)+C(x+2)$$

El valor de A es encontrado al comparar a los coeficientes de los términos con $latex x^2$ y encontramos que $latex A=2$.

Para encontrar el valor de B, sustituimos $latex x=-2$ y tenemos:

$$2(-2)^2-2-5=A(-2+2)(-2+1)+B(-2+1)+C(-2+2)$$

$latex 1=-B$

$latex B=-1$

Para encontrar el valor de C, sustituimos $latex x=-1$ y tenemos:

$$2(-1)^2-1-5=A(-1+2)(-1+1)+B(-1+1)+C(-1+2)$$

$latex -4=C$

$latex C=-4$

Entonces, tenemos:

$$\frac{2x^2+x-5}{(x+2)(x+1)}=2-\frac{1}{x+2}-\frac{4}{x+1}$$

El grado del polinomio en el numerador es 4 y el grado del polinomio en el denominador es 3. Entonces, el cociente será un polinomio de grado 4-3=1.

Entonces, el cociente es polinomio lineal y sus fracciones parciales tienen la siguiente forma:

$$\frac{3x^4+7x^3+8x^2+53x-186}{(x+4)(x^2+9)}=Ax+B+\frac{C}{x+4}+\frac{Dx+E}{x^2+9}$$

Cuando multiplicamos a toda la expresión por $latex (x+4)(x^2+9)$, tenemos:

$$3x^4+7x^3+8x^2+53x-186=(Ax+B)(x+4)(x^2+9)+C(x^2+9)+(Dx+E)(x+4)$$

El valor de A es encontrado al comparar los coeficientes de los términos con $latex x^4$ y encontramos que $latex A=3$.

Comparando los coeficientes del término $latex x^3$, tenemos:

$latex 7=4A+B$

Sustituyendo $latex A=3$, encontramos que $latex B=-5$.

Cuando usamos el valor $latex x=-4$, tenemos:

$$3(-4)^4+7(-4)^3+8(-4)^2+53(-4)-186=C((-4)^2+9)$$

$latex 50=25C$

$latex C=2$

Comparando los coeficientes del término $latex x^2$, tenemos:

$$8=9A+4B+C+D$$

Sustituyendo los valores $latex A=4$, $latex B=-5$ y $latex C=2$, tenemos $latex D=-1$.

Finalmente, comparando los términos constantes, tenemos:

$latex -186=36B+9C+4E$

Sustituyendo los valores $latex B=-5$ y $latex C=2$, tenemos $latex E=-6$.

Entonces, tenemos:

$$\frac{3x^4+7x^3+8x^2+53x-186}{(x+4)(x^2+9)}=3x-5+\frac{2}{x+4}+\frac{-x-6}{x^2+9}$$