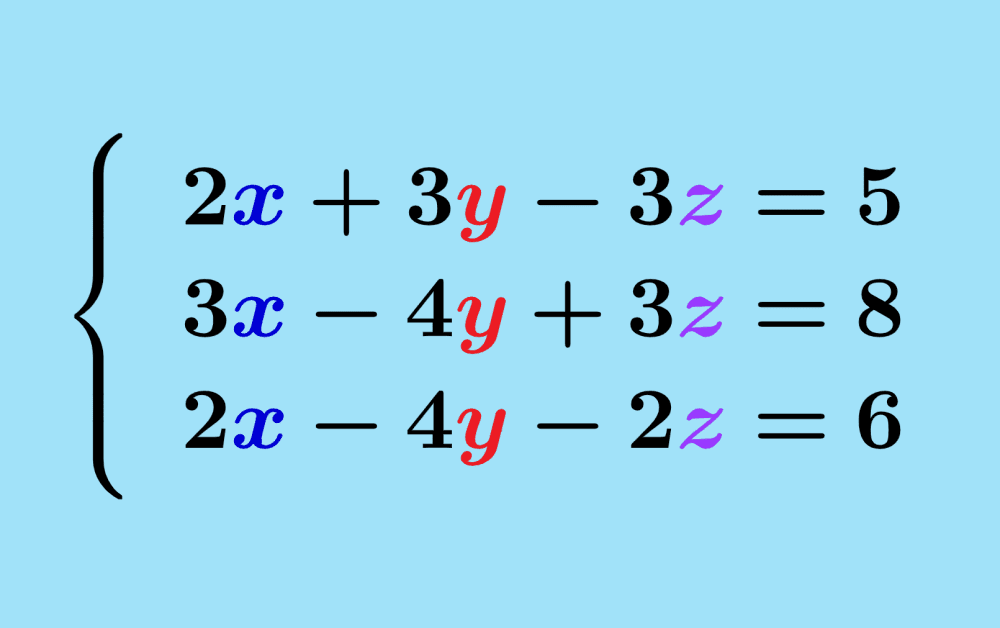Un sistema de ecuaciones 3×3 es un sistema formado por tres ecuaciones con tres variables. Existen varios métodos para resolver un sistema de ecuaciones 3×3, como la representación gráfica, la sustitución y la eliminación Gaussiana.
En este artículo, aprenderemos a resolver sistemas de ecuaciones 3×3 usando los métodos de sustitución y eliminación. Veremos varios ejercicios resueltos para aprender sobre este tema.
¿Cómo resolver sistemas de ecuaciones 3×3?
Para resolver un sistema de tres ecuaciones con tres variables, puedes utilizar uno de varios métodos. Aquí tienes dos enfoques comunes:
- Eliminación gaussiana: Este método consiste en sumar o restar ecuaciones para eliminar variables, de una en una, hasta que el sistema se encuentre en lo que se conoce como forma reducida fila-echelón. Una vez que el sistema está en esta forma, es fácil resolver las variables.
- Regla de Cramer: Este método consiste en expresar la solución en términos de determinantes de determinadas matrices. Para utilizar la regla de Cramer, es necesario poder calcular determinantes, lo que puede resultar un poco más complicado que los métodos utilizados en la eliminación de Gauss.
He aquí un ejemplo de cómo resolver un sistema de tres ecuaciones con tres variables utilizando la eliminación de Gauss:
Supongamos que tenemos el siguiente sistema:
$$\begin{cases} 3x + 4y – 2z = 0\\2x – 3y + 4z = 11\\x – 2y + 3z = 7 \end{cases}$$
Podemos empezar eliminando la variable x de la segunda y tercera ecuaciones. Para ello, multiplicamos la segunda ecuación por 1 y la tercera ecuación por -2, y luego sumamos las ecuaciones resultantes:
$$\begin{cases} 2x – 3y + 4z = 11\\-2x + 4y -6z = -14 \end{cases}$$
____________________
$latex y-2z=-3$
Luego, podemos eliminar la variable x de las ecuaciones primera y tercera, multiplicando la primera ecuación por 1 y la tercera ecuación por -3, y sumando después las ecuaciones resultantes:
$$\begin{cases} 3x+4y-2z=0\\-3x+6y-9z=-21 \end{cases}$$
____________________
$latex 10y-11z=-21$
Por último, podemos multiplicar a la ecuación $latex y-2z=-3$ por -10 y sumar estas dos ecuaciones para eliminar la variable y:
$$\begin{cases} -10y+20z=30\\10y-11z=-21 \end{cases}$$
____________________
$latex 9z=9$
Resolviendo esta ecuación para z, encontramos que $latex z = 1$.
Sustituyendo este valor en la ecuación $latex y-2z=-3$, podemos resolver para y: $latex y = -1$.
Sustituyendo estos valores de nuevo en las ecuaciones originales, podemos resolver para x: $latex x = 2$.
Por lo tanto, la solución del sistema es $latex x = 2$, $latex y = -1$ y $latex z = 1$.
Ejercicios resueltos de sistemas de ecuaciones 3×3
EJERCICIO 1
Encuentre la solución del siguiente sistema de tres ecuaciones con tres incógnitas por el método de sustitución:
$$\begin{cases} x+y-2z=1\\2x-4y+z=0\\2y-3z=-1 \end{cases}$$
Solución
Numeramos las ecuaciones como (i), (ii), (iii):
$$\begin{cases} \text{(i)}~~ x+y-2z=1\\\text{(ii)}~~ 2x-4y+z=0\\ \text{(iii)}~~2y-3z=-1 \end{cases}$$
De la tercera (iii) despejamos z:
$latex z=\frac{2}{3}y+\frac{1}{3} $
Sustituimos z en (ii) para obtener (ii’):
$$2x-4y+\frac{2}{3}y+\frac{1}{3}=\ 2x-\frac{10}{3}y+\frac{1}{3}=0 \; \; \text{(ii’)}$$
También sustituimos z en (i) para obtener (i’):
$$ x+y-2(\frac{2}{3}y+\frac{1}{3})=\, x-\frac{1}{3}y-\frac{2}{3}=1 \; \; \text{(i’)} $$
De la ecuación anterior (i’) despejamos y: $latex y=3x-5 $.
Sustituyendo y en (ii’) nos queda: $latex 17-8x=0$. Despejando nos queda:
$$ x=\frac{17}{8}$$
Sustituimos el valor encontrado de x en (i’) y despejamos y: $latex \frac{17}{8}-\frac{1}{3}y-\frac{2}{3}=1$
para obtener:
$$y=\frac{11}{8}$$
Finalmente, sustituimos x e y en la ecuación (i) y despejamos z:
$$\frac{17}{8}+\frac{11}{8}-2z=1$$
$$z=\frac{5}{4}$$
Resumiendo, la solución del sistema planteado es:
$$\left[ x=\frac{17}{8},y=\frac{11}{8},z=\frac{5}{4}\right] $$
EJERCICIO 2
Sea el siguiente sistema de ecuaciones tres ecuaciones lineales
con tres incógnitas:
$$\begin{cases} \text{(i)}~~x+y+z=6 \\ \text{(ii)}~~x-y+2z=5 \\ \text{(iii)}~~x-y-3z=-10 \end{cases}$$
demuestre, por el método de eliminación, que su solución es: $latex \left[ x=1,y=2,z=3 \right] $.
Solución
Restando (i) menos (ii) obtenemos: $latex 2y-z=1 $
Restando (ii) menos (iii) se obtiene: $latex 5z=15 $
De donde se deduce que: $latex z=3 $
Sustituyendo en la penúltima expresión nos queda: $latex 2y-3=1 $, cuya
solución es: $latex y=2 $
Por último, sustituimos los valores obtenidos en la ecuación (i): $latex x+2+3=6 $
obteniéndose: $latex x=1 $.
EJERCICIO 3
Sea el siguiente sistema de tres ecuaciones lineales
con tres incógnitas:
$$\begin{cases} \text{(i)}~~2x+3y+z=1 \\ \text{(ii)}~~6x-2y-z=-14 \\ \text{(iii)}~~3x+y-z=1 \end{cases}$$
Hallar los valores de x, y, z que satisfacen el sistema.
Solución
Aplicaremos el método de eliminación.
Multiplicamos a la ecuación (i) por 3 y a la ecuación (ii) por -1 y las sumamos:
$$3(2x+3y+z)-(6x-2y-z)=3(1)-(-14) $$
Se cancela x obteniéndose: $latex 11y+4z=17 $ (I)
Multiplicamos a la ecuación (ii) por 1 y la ecuación (iii) por -2 y las sumamos:
$$ (6x-2y-z)-2(3x+y-z)=(-14)-2(1) $$
Se elimina x para obtener: $latex z-4y=-16 $ (II)
Restamos (I) menos 4(II):
$$(11y+4z)-4(z-4y)=(17)-4(-16)$$
Se elimina z para tener: $latex 27y=81 $ (III)
De la ec.(III) despejamos y: $latex 27y=81 $, y se obtiene: $latex y=3 $
Sustituimos el valor obtenido de y en (II): $latex z-4(3)=-16 $, cuya solución es: $latex z=-4 $
Por último, sustituimos los valores obtenidos para z e y en (i): $latex 2x+3(3)+(-4)=1 $
Despejando x: $latex 2x+3(3)+(-4)=1$, se obtiene: $latex x=-2 $
Resumiendo, la solución del sistema de ecuaciones es: $latex \left[ x=-2,y=3,z=-4\right] $
EJERCICIO 4
Sea el siguiente sistema de tres ecuaciones con tres incógnitas:
$$\begin{cases} \text{(i)}~~\frac{x}{2}+\frac{y}{2}-\frac{z}{3}=3 \\ \text{(ii)}~~ \frac{x}{3}+\frac{y}{6}-\frac{z}{2}=-5 \\ \text{(iii)}~~\frac{x}{6}-\frac{y}{3}+\frac{z}{6}=0 \end{cases}$$
Obtener la solución por el método de sustitución.
Solución
De la (iii) despejamos z: $latex \frac{x}{6}-\frac{y}{3}+\frac{z}{6}=0 $,
Obteniéndose: $latex z=2y-x $ (iii’)
Sustituimos en la (ii): $latex \frac{x}{3}+\frac{y}{6}-\frac{2y-x}{2}=-5 $
y despejamos y: $latex y=x+6 $ (ii’)
Sustituimos (ii’) en (iii’): $latex z=2(x+6)-x=\; x+12 $ es decir: $latex z=x+12 $ (iv)
Se reemplaza los valores obtenidos en (ii’) y (iv) en la ecuación (i):
$$\frac{x}{2}+\frac{x+6}{2}-\frac{x+12}{3}=3 $$
Y se despeja la variable x: $latex x=6 $
Ahora se sustituye el valor obtenido en (ii’) y se calcula y: $latex y=6+6=12 $
Por ultimo, se sustituye el valor de x en (iv):$latex z=6+12=18 $
En resumen, la solución del sistema de ecuaciones es: $latex \left[ x=6,y=12,z=18 \right] $
EJERCICIO 5
Hallar las soluciones del siguiente sistema de ecuaciones:
$$\begin{cases} \text{(i)}~~x+y=5 \\ \text{(ii)}~~ x+z=6 \\ \text{(iii)}~~ y+z=7 \end{cases}$$
Solución
Restando (i) menos (ii) obtenemos:
$latex y-z=-1$ (ii’)
Restando la ecuación anterior (ii’) menos (iii) se obtiene:
$$-2z=-8$$
De donde se deduce que: $latex z=4$
Sustituyendo el valor obtenido para z en la ec.(iii) nos queda:
$latex y+4=7$, de donde se obtiene: $latex y=3$
Finalmente, se sustituye el valor obtenido de y en (i):
$latex x+3=5$, de donde se obtiene: $latex x=2$
En resumen, el sistema de ecuaciones planteado tiene soluciones:
$$\left[ x=2,y=3,z=4\right] $$
EJERCICIO 6
Resolver el siguiente sistema de ecuaciones:
$$\begin{cases} \text{(i)}~~3x+2y=2 \\ \text{(ii)}~~ 2y+2z=\frac{3}{2} \\ \text{(iii)}~~x+4z=\frac{4}{3} \end{cases}$$
Solución
Aplicaremos el método de eliminación.
Restando la ecuación (ii) de la (i):
$$(3x+2y=2)-\left(2y+2z= \frac{3}{2} \right)$$
==> $latex 3x-2z = \dfrac{1}{2}$ (I)
2(I) + (iii):
$$2(3x-2z=\frac{1}{2})+\left(x+4z=\frac{4}{3}\right)$$
==> $latex 7x=\frac{7}{3}$
==> $latex x=\frac{1}{3}$
Sustituimos $latex x=\frac{1}{3}$ en (i):
$latex 3(\frac{1}{3})+2y=2$ ==> $latex 2y+1=2$,
obteniéndose: $latex y=\frac{1}{2}$
El valor obtenido de y se sustituye en (ii): $latex 2(\frac{1}{2})+2z=3/2$
y nos queda: $latex z=\frac{1}{4}$
Resumiendo, la solución del sistema de ecuaciones es:
$$\left[ x=\frac{1}{3},y=\frac{1}{2},z=\frac{1}{4}\right] $$
EJERCICIO 7
Hallar los valores de las variables u, v y w en el siguiente sistema de ecuaciones:
$$\begin{cases} \text{(i)}~~\frac{1}{u}+\frac{1}{v}=5 \\ \text{(ii)}~~ \frac{1}{u}+\frac{1}{w}=6 \\ \text{(iii)}~~\frac{1}{v}+\frac{1}{w}=7 \end{cases}$$
Solución
Comenzamos por hacer el siguiente cambio de variable:
$$x=\frac{1}{u}$$
$$y=\frac{1}{v}$$
$$z=\frac{1}{w}$$
Para obtener:
$$\begin{cases} \text{(i)}~~x+y=5 \\ \text{(ii)}~~ x+z=6 \\ \text{(iii)}~~y+z=7 \end{cases}$$
La solución de este sistema es: $latex \left[ x=2,y=3,z=4\right] $ (ver ejercicio 5)
Ahora se invierte el cambio de variable que se hizo anteriormente:
$latex u=\frac{1}{x}$ sustituyendo el x=2 se obtiene: $latex u=\frac{1}{2}$
$latex v=\frac{1}{y}$ sustituyendo el y=3 se obtiene: $latex v=\frac{1}{3}$
$latex w=\frac{1}{z}$ sustituyendo el z=4 se obtiene: $latex w=\frac{1}{4}$
EJERCICIO 8
Resuelva el siguiente sistema de ecuaciones:
$$\begin{cases} \text{(i)}~~ \frac{3}{u}+\frac{2}{v}=2 \\ \text{(ii)}~~\frac{2}{v}+\frac{2}{w}=\frac{3}{2} \\ \text{(iii)}~~ \frac{1}{u}+\frac{4}{w}=\frac{4}{3} \end{cases}$$
Solución
Se hace el siguiente cambio de variable:
$$ x=\frac{1}{u}$$
$$y=\frac{1}{v}$$
$$z=\frac{1}{w}$$
Para obtener:
$$\begin{cases} \text{(i)}~~ 3x+2y=2 \\ \text{(ii)}~~2y+2z=\frac{3}{2} \\ \text{(iii)}~~ x+4z=\frac{4}{3} \end{cases}$$
cuya solución es: $latex \left[ x=\frac{1}{3},y=\frac{1}{2},z=\frac{1}{4}\right] $ (ver ejercicio 6)
Ahora se invierte el cambio de variable que se hizo anteriormente:
$latex u=\frac{1}{x}$ sustituyendo el x=1/3 se obtiene: $latex u=3$
$latex v=\frac{1}{y}$ sustituyendo el y=1/2 se obtiene: $latex v=2$
$latex w=\frac{1}{z}$ sustituyendo el z=1/4 se obtiene: $latex w=4$
EJERCICIO 9
Hallar los valores de x, y y z que satisfacen simultáneamente a las tres ecuaciones dadas:
$$\begin{cases} \text{(i)}~~x+y=1 \\ \text{(ii)}~~y+z=-1 \\ \text{(iii)}~~x+z=-6 \end{cases}$$
Solución
El procedimiento de reducción consiste en operaciones de suma, resta y multiplicación de constantes en las ecuaciones dadas, y en las que se obtengan, reduciendo el número de incógnitas, hasta una ecuación en la que solo aparezca una incógnita a despejar.
Restando (i) menos (ii) :
$latex (x+y=1)-(y+z=-1)$ obtenemos: $latex x-z=2$ (ii’)
Sumando la ecuación anterior (ii’) mas (iii) :
$latex(x-z=2)+(x+z=-6)$ se tiene: $latex 2x=-4$
De donde se deduce que: $latex x=-2$
Sustituyendo el valor obtenido para x en la ec.(i) nos queda:
$latex -2+y=1$, de donde se obtiene: $latex y=3$
Finalmente, se sustituye el valor obtenido de y en (ii):
$latex 3+z=-1$, de donde se obtiene: $latex z=-4$
En resumen, el sistema de ecuaciones planteado tiene soluciones:
$$\left[ x=-2,y=3,z=-4\right] $$
EJERCICIO 10
Resuelva el siguiente sistema de ecuaciones:
$$\begin{cases} \text{(i)}~~ 5x-3z=2 \\ \text{(ii)}~~ -y+2z=-5 \\ \text{(iii)}~~ x+2z=8 \end{cases}$$
Solución
Aplicaremos el metodo de eliminacion.
2(i) + 3(ii):
$$2(5x-3z=2)+3(-y+2z=-5)$$
==> $latex 10x-3y=-11$ (I)
(ii) – (iii):
$$(-y+2z=-5)-(x+2z=8)$$
==> $latex x+y=13$ (II)
(I)+3(II):
$$(10x-3y=-11)+3(x+y=13)$$
que se reduce a: $latex13x=28$, obteniéndose: $latex x=\frac{28}{13}$
Sustituimos $latex x=\frac{28}{13}$ en (iii): $latex \frac{28}{13}+2z=8$, cuya solución es: $latex z=\frac{38}{13}$
El valor obtenido de z se sustituye en (ii): $latex -y+2(\frac{38}{13})=-5$, y nos queda: $latex y=\frac{141}{13}$
Resumiendo, la solución del sistema de ecuaciones es:
$$\left[ x=\frac{28}{13},y=\frac{141}{13},z=\frac{38}{13}\right]$$
Ejercicios de sistemas de ecuaciones 3×3 para resolver
Encuentra el valor de x en el sistema de ecuaciones: $$\begin{cases} 2x-2y+z=-5 \\ 3x+y+3z=-1 \\ 4x-y-2z=-12 \end{cases}$$
Escribe el valor de x en la casilla.
Véase también
¿Interesado en aprender más sobre sistemas de ecuaciones? Puedes mirar estas páginas: