Para saber si una función es simétrica, debemos observar su gráfica e identificar algunas características que son únicas de funciones simétricas. Por ejemplo, la gráfica puede tener una reflexión en el eje x, en el eje y o puede tener una simetría rotacional con respecto al origen.
En este artículo, miraremos los diferentes tipos de simetría con ejemplos para ilustrar las ideas.
ÁLGEBRA
Relevante para…
Aprender a determinar si es que una función tiene algún tipo de simetría.
ÁLGEBRA
Relevante para…
Aprender a determinar si es que una función tiene algún tipo de simetría.
¿Cómo saber si una gráfica es simétrica?
Podemos saber si es que una gráfica es simétrica con respecto a una línea o a un punto si es que la gráfica no cambia cuando es reflejada con respecto a esa línea o es rotada alrededor de ese punto.
La simetría puede ser útil cuando queremos graficar una ecuación, ya que nos dice que si es que conocemos una porción de la gráfica, entonces también conoceremos la porción simétrica restante de la gráfica.
Podemos distinguir tres tipos principales de simetría:
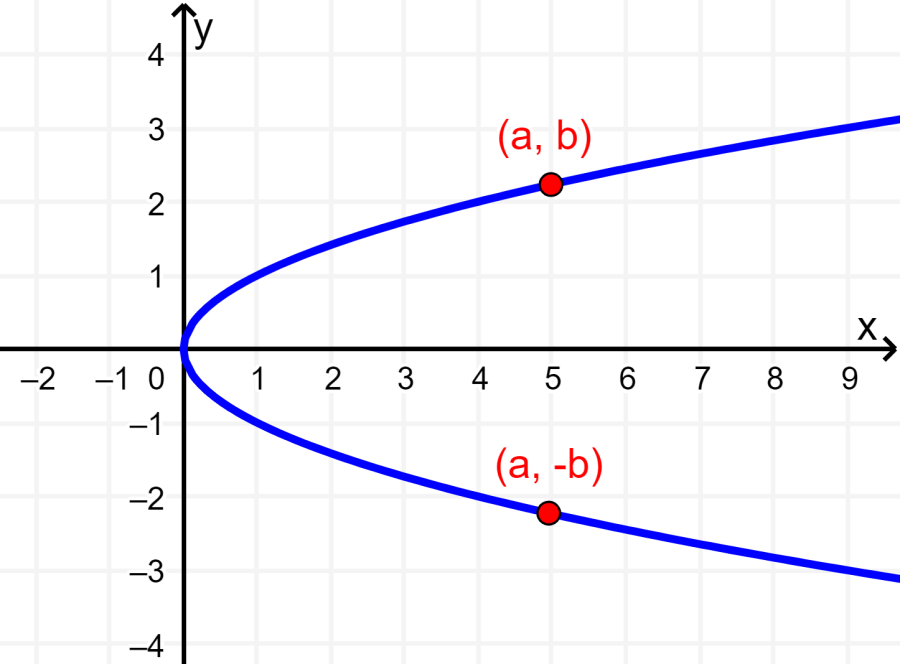
1. Una gráfica tiene simetría con respecto al eje x si es que cuando tenemos a (a, b) en la gráfica, también tenemos a (a, -b). La siguiente es una gráfica con simetría con respecto al eje x:
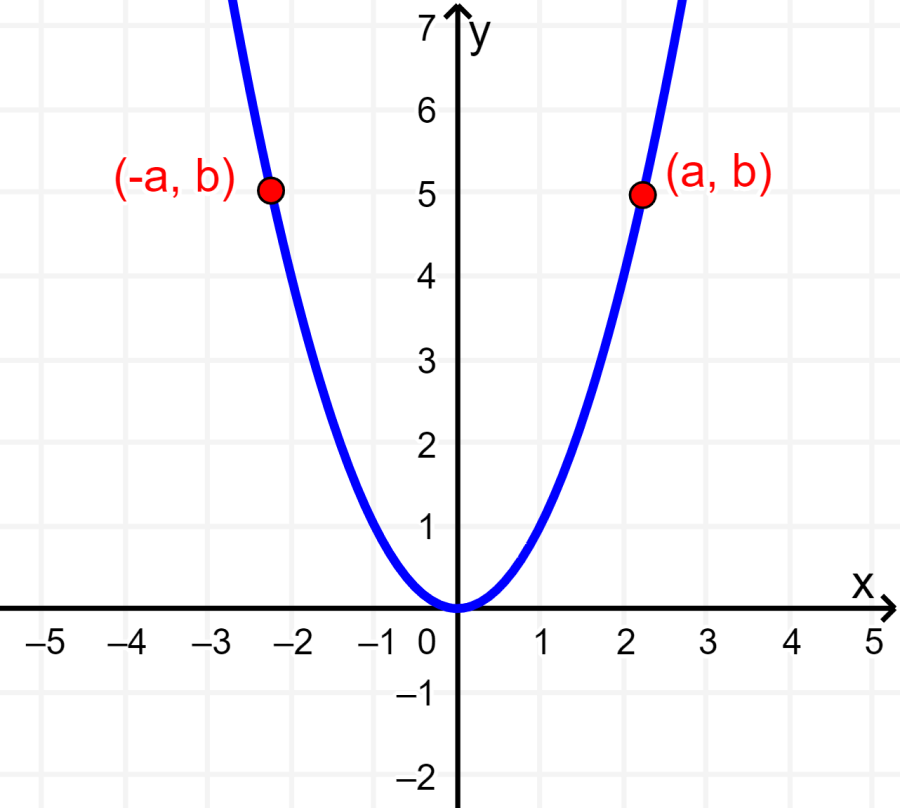
2. Una gráfica tiene simetría con respecto al eje y si es que cuando tenemos el punto (a, b) en la gráfica, también tenemos a (-a, b). La siguiente es una gráfica con simetría con respecto al eje y:
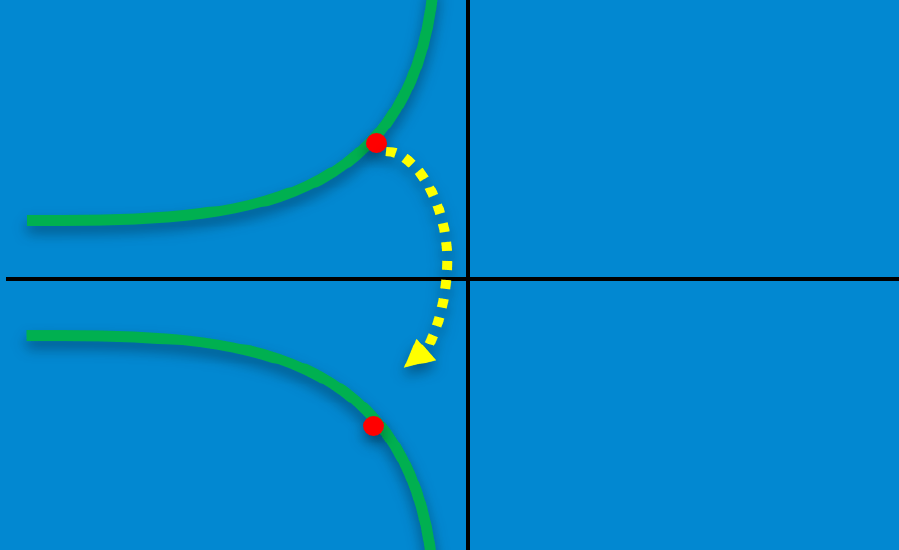
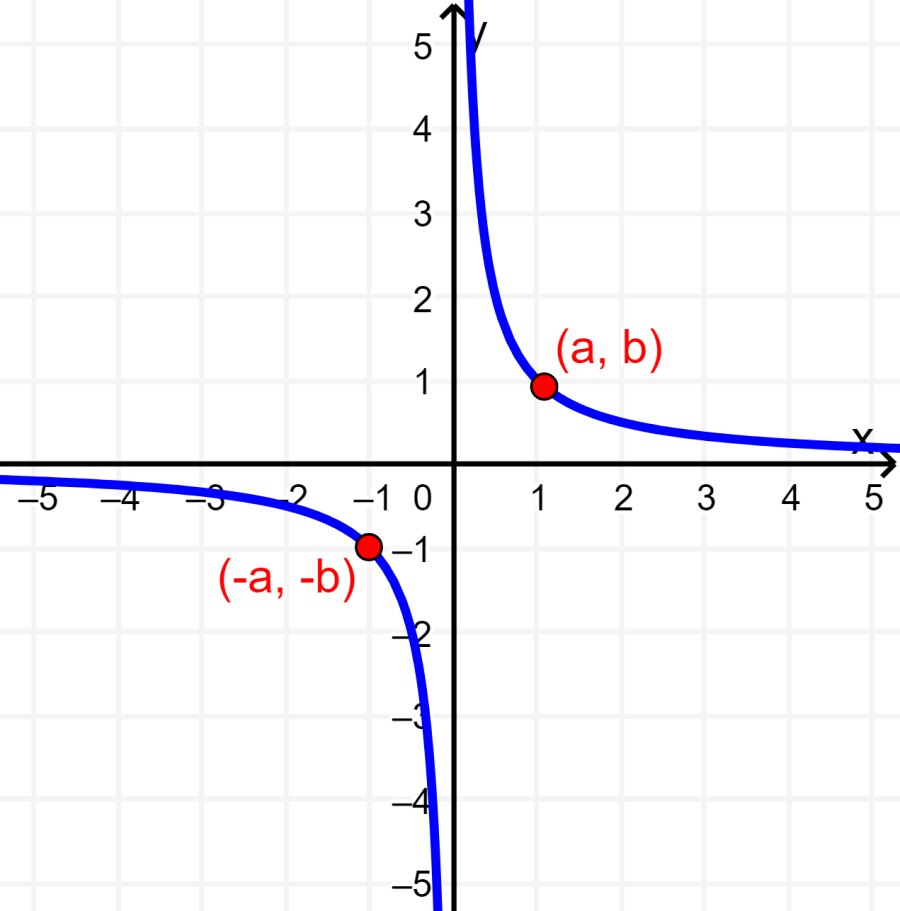
3. Una gráfica tiene simetría con respecto al origen si es que cuando tenemos el punto (a, b) en la gráfica, también tenemos a (-a, -b). La siguiente es una gráfica que tiene simetría con respecto al origen:
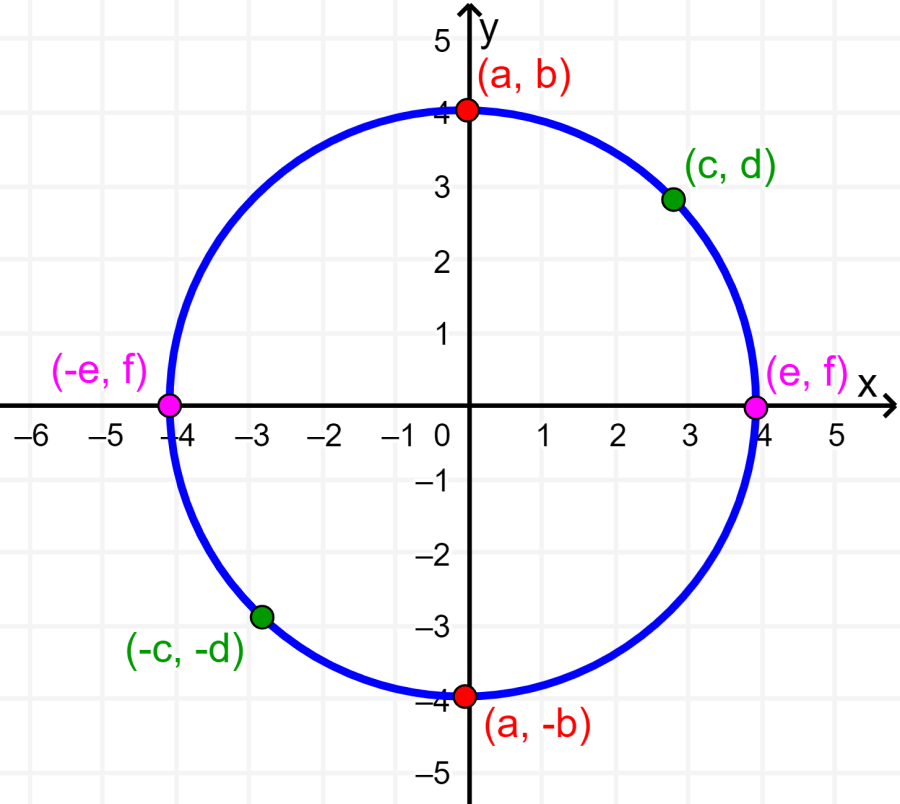
Ten en cuenta que la mayoría de las gráficas no tienen ningún tipo de simetría. Además, también es posible que una gráfica tenga más de un tipo de simetría. Por ejemplo, la gráfica de un círculo centrado en el origen tiene los tres tipos de simetrías al mismo tiempo:
¿Cómo saber si una función tiene simetría par o impar?
Podemos distinguir dos tipos de simetrías de gráficas de funciones:
Simetría de reflexión con respecto al eje y. Esto sucede cuando tenemos $latex f(x)=f(-x)$.
Simetría de rotación con respecto al origen. Esto sucede cuando tenemos $latex f(-x)=-f(x)$.
Observamos que las funciones como $latex f(x)={{x}^2}$ y $latex f(x)={{x}^4}$, en donde el exponente de x es par, tendrán la propiedad que $latex f(x)=f(-x)$ dado que -1 elevado a un exponente par es igual a 1.
De igual forma, las funciones como $latex f(x)=x$ y $latex f(x)={{x}^3}$, en donde el exponente en x es impar, tendrán la propiedad que $latex f(-x)=-f(x)$ dado que -1 elevado a un exponente impar es igual a -1.
Entonces, tenemos las siguientes definiciones:
Una función es par si es que $latex f(-x)=f(x)$. Una función par tiene una reflexión con respecto al eje y.
Una función es impar si es que $latex f(-x)=-f(x)$. Una función impar tiene simetría rotacional con respecto al origen.
Podemos decidir algebraicamente si es que una función es par, impar o ninguna al reemplazar la x por -x y calcular $latex f(-x)$. Si es que tenemos $latex f(-x)=f(x)$, la función es par. Si es que tenemos $latex f(-x)=-f(x)$, la función es impar.
¿Cómo saber si una función es simétrica respecto al origen?
La simetría con respecto al origen es tal vez la más difícil de identificar. Para saber si una función es simétrica respecto al origen podemos identificar varios puntos en la gráfica ya que, en una gráfica de función con simetría respecto al origen tenemos el punto (a, b) y el punto (-a, -b).
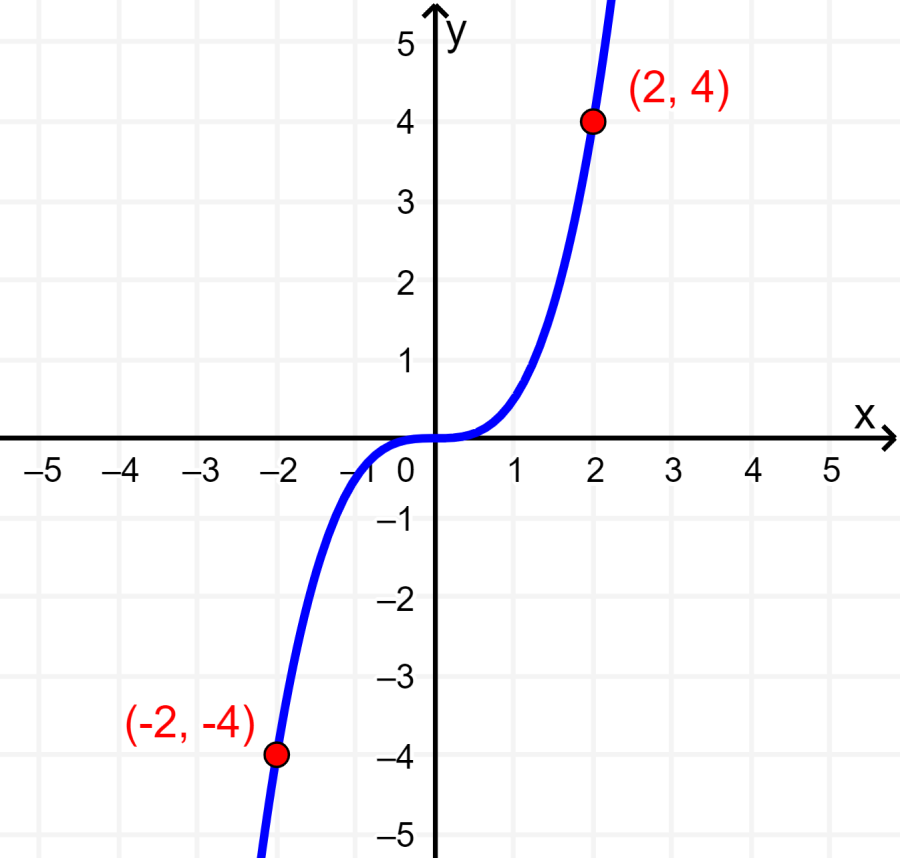
Por ejemplo, en la siguiente gráfica tenemos los puntos (2, 4) y (-2, -4). Esto significa que la gráfica sí es simétrica con respecto al origen.
Prueba para simetría con respecto al origen
Una gráfica tendrá simetría con respecto al origen si es que obtenemos una ecuación equivalente cuando todas las y son reemplazadas por -y y todas las x son reemplazadas por –x.
EJEMPLO
- Determina si es que la función $latex y=2{{x}^3}-{{x}^5}$ tiene simetría con respecto al origen.
Respuesta: Reemplazamos x con -x y reemplazamos y con -y.
$latex y=2{{x}^3}-{{x}^5}$
$latex -y=2{{(-x)}^3}-{{(-x)}^5}$
$latex -5=-2{{x}^3}+{{x}^5}$
Podemos ver que todos los signos de esta expresión son exactamente opuestos a los de la expresión original. Esto significa que esta expresión es equivalente a la expresión original ya que simplemente podemos multiplicar toda la expresión por -1 para obtener la expresión original.
Ejemplos de gráficas con simetría
En la descripción de las siguientes gráficas se muestra si es que hay alguna simetría y se indica si es que la gráfica representa a una función.
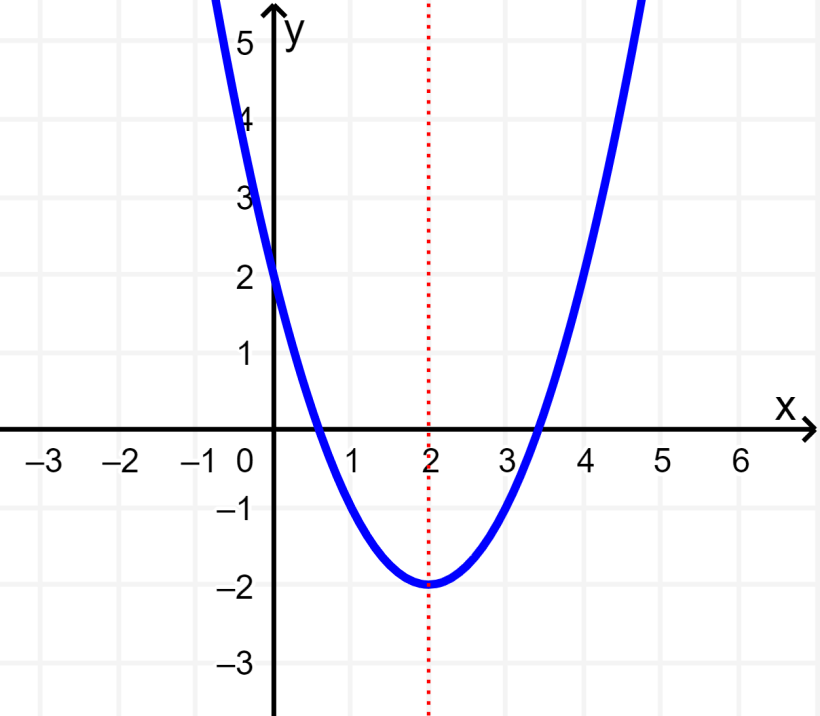
La siguiente gráfica es simétrica con respecto a su eje, es decir, es simétrica con respecto a la línea x=2. No hay ninguna otra simetría. La gráfica sí representa a una función.
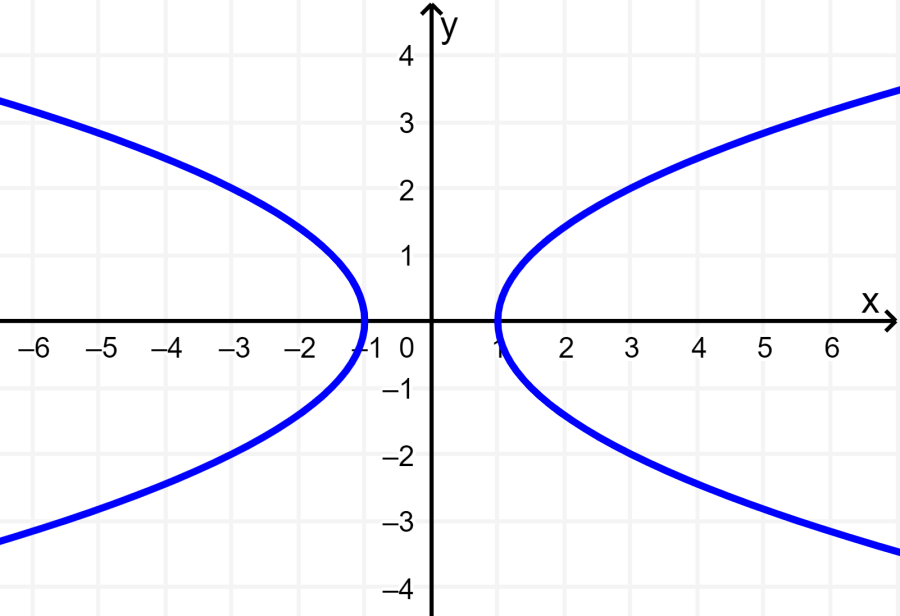
La siguiente gráfica es simétrica con respecto al eje x y al eje y. Esta gráfica también es simétrica con respeto al origen. Dado que la gráfica no pasa la prueba de la línea vertical, es decir, una línea vertical puede ser trazada que pase por más de un punto en la gráfica, entonces, la gráfica no representa a una función.
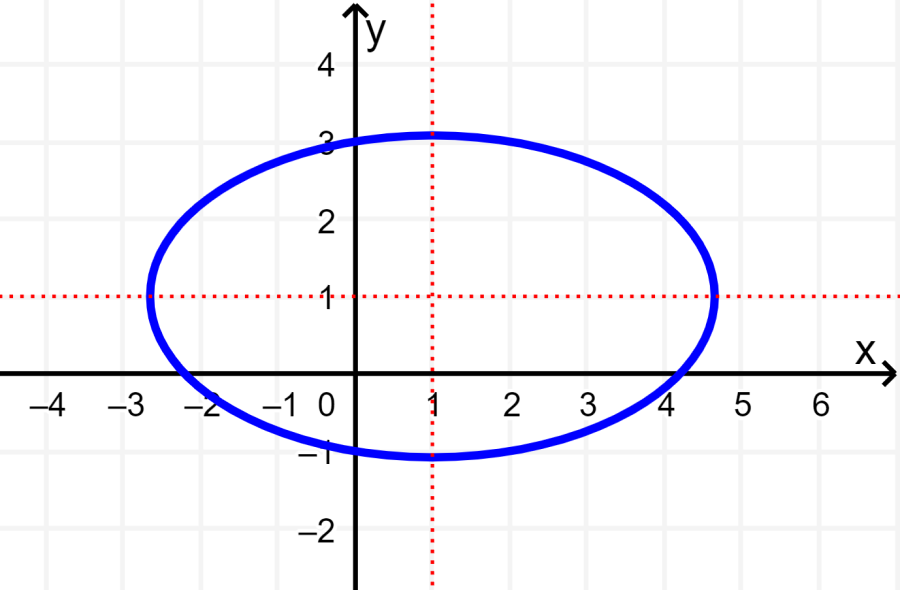
Esta gráfica es simétrica con respecto a las líneas x=1 y y=1. Dado que una línea vertical puede ser trazada que pasa por más de un punto en la gráfica, la gráfica no representa a una función.
La siguiente gráfica representa a una función cúbica que es simétrica con respecto al punto (1, -2). Esta gráfica sí representa a una función.
En la descripción de las siguientes gráficas se muestra si es que la función es par, impar o ninguna.
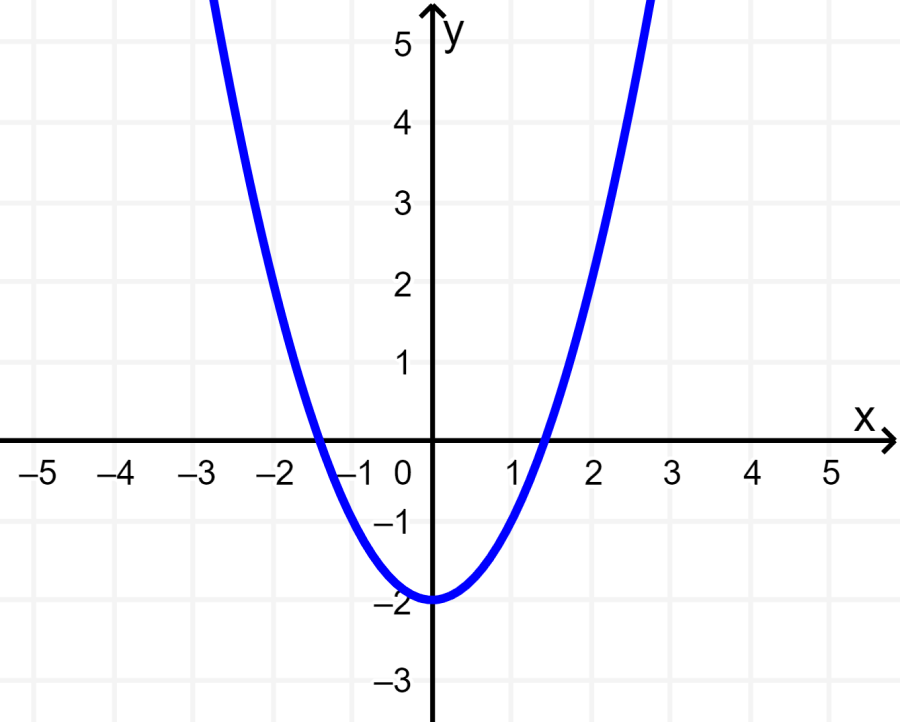
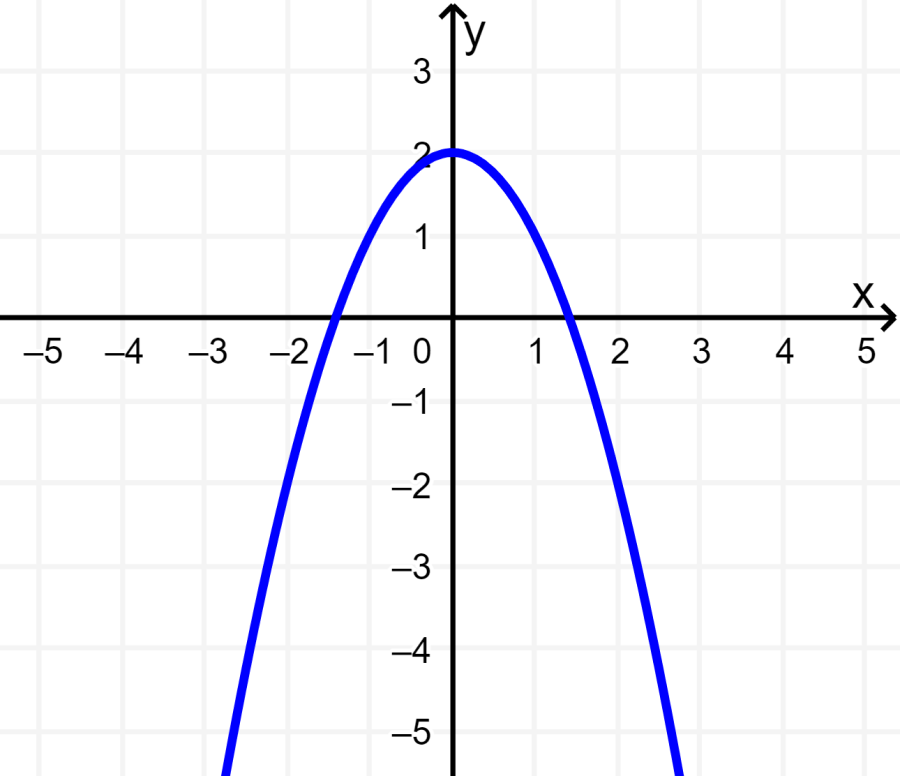
La siguiente parábola tiene el vértice en el eje y, por lo que el eje de simetría es el eje y. Esto significa que la función es par.
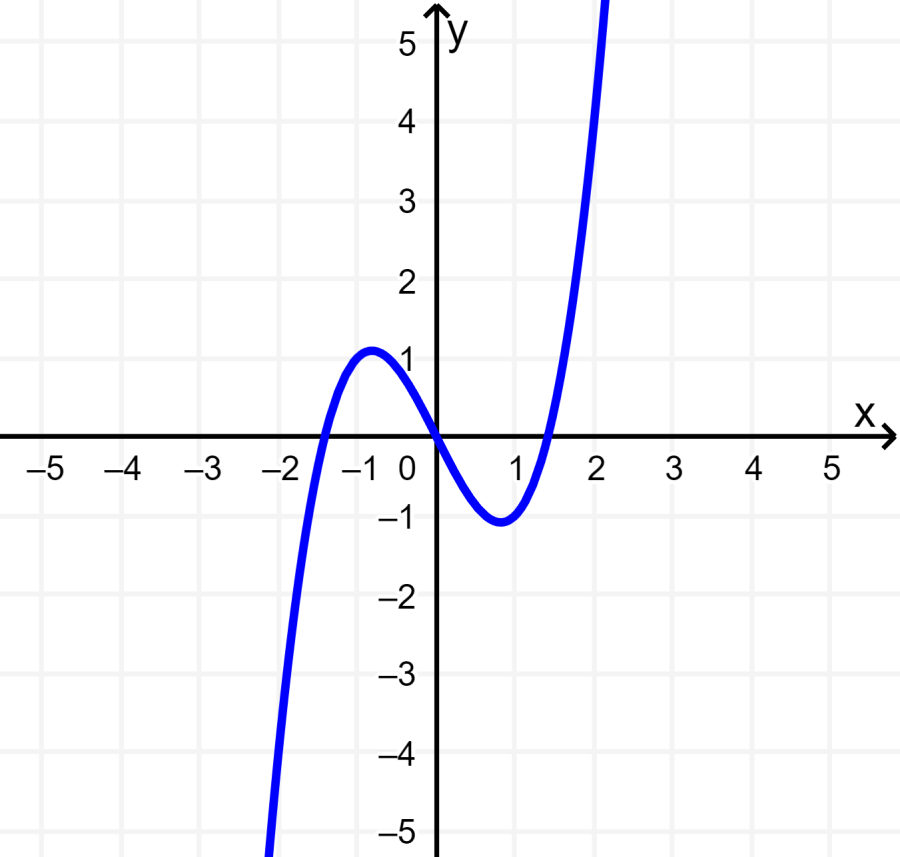
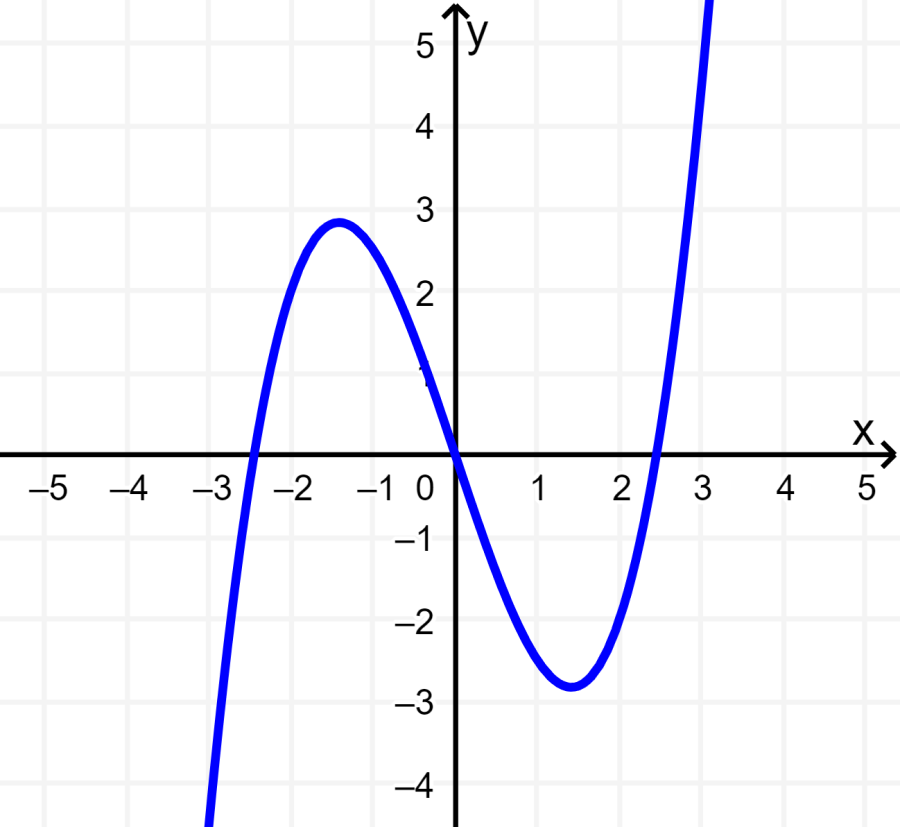
La siguiente función cúbica está centrada en el origen y si es que la giramos 180°, obtendremos la misma gráfica. Esto significa que la función es impar.
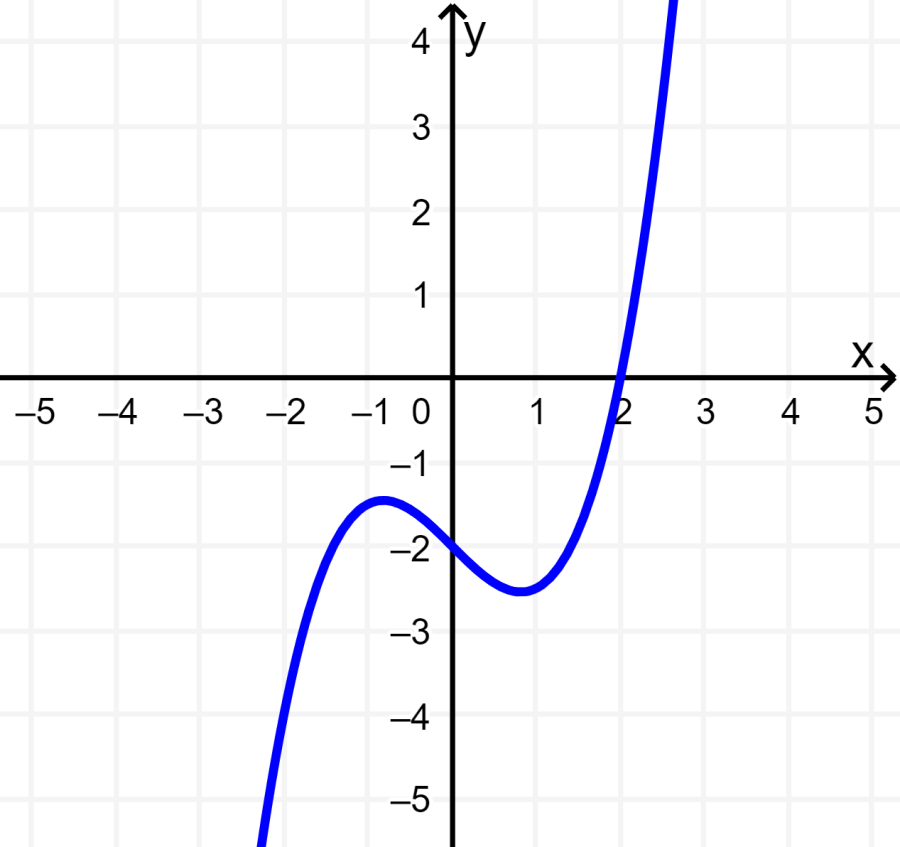
La siguiente función cúbica está centrada en el punto (0, -2). Esta función es simétrica, pero no con respecto al origen o el eje y. Por lo tanto, esta función no es ni par ni impar.
Ejercicios de simetría de funciones resueltos
EJERCICIO 1
Determina si es que la función $latex f(x)=2{{x}^2}+5$ es simétrica.
Solución
Prueba 1: Empezamos verificando si es que la función es simétrica con respecto al eje y. Eso significa que tenemos que reemplazar todas las x con –x:
$latex f(-x)={{(-x)}^2}+5$
$latex ={{x}^2}+5$
Después de simplificar, obtuvimos exactamente la misma función que $latex f(x)$, lo que significa que ambas son equivalentes. Entonces, esta ecuación sí es simétrica con respecto al eje y.
Prueba 2: Ahora, verificamos por simetría con respecto al origen. Esto requiere que remplacemos tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$.
$latex -f(-x)={{(-x)}^2}+5$
$latex -f(-x)={{x}^2}+5$
En este caso, el lado derecho de la función es idéntico a la original, pero el lado izquierdo es diferente, ya que tenemos un signo menos en frente.
EJERCICIO 2
Determina si es que la función $latex f(x)={{x}^3}+5x$ tiene algún tipo de simetría.
Solución
Prueba 1: Para determinar si es que la función es simétrica con respecto al eje y, tenemos que reemplazar todas las x con –x:
$latex f(-x)={{(-x)}^3}+5(-x)$
$latex =-{{x}^3}-5x$
Vemos que obtuvimos una expresión diferente a la función original en la parte derecha. Esto significa que la función no es simétrica con respecto al eje y.
Prueba 2: Para verificar si la función es simétrica con respecto al origen, tenemos que cambiar tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$.
$latex -f(-x)={{(-x)}^3}+5(-x)$
$latex -f(-x)=-{{x}^3}-5x$
$latex f(-x)={{x}^3}+5x$
Vemos que obtuvimos signos negativos de ambos lados. Al multiplicar ambos lados por -1, obtuvimos la función original. Esto significa que la función sí es simétrica con respecto al origen.
EJERCICIO 3
¿Tiene la función $latex f(x)={{x}^4}+2{{x}^3}+2x$ algún tipo de simetría?
Solución
Prueba 1: Buscamos la simetría con respecto al eje y al reemplazar todas las x con –x:
$latex f(-x)={{(-x)}^4}+2{{(-x)}^3}+2(-x)$
$latex ={{x}^4}-2{{x}^3}-2x$
Después de simplificar, obtuvimos una expresión diferente a la función original, $latex f(x)$. Por lo tanto, esta ecuación no tiene simetría con respecto al eje y.
Prueba 2: Buscamos simetría con respecto al origen al reemplazar tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$.
$latex -f(-x)={{(-x)}^4}+2{{(-x)}^3}+2(-x)$
$latex -f(-x)={{x}^4}-2{{x}^3}-2x$
$latex f(-x)=-{{x}^4}+2{{x}^3}+2x$
Si es que multiplicamos ambos lados de la función por -1, no obtenemos la función original, por lo que esta función no tiene simetría con respecto al origen.
EJERCICIO 4
Determina si la función $latex f(x)=3{{x}^4}-2{{x}^2}+4$ tiene algún tipo de simetría.
Solución
Prueba 1: Empezamos buscando simetría con respecto al eje y. Eso significa que tenemos que reemplazar todas las x con –x:
$latex f(-x)=3{{(-x)}^4}-2{{(-x)}^2}+4$
$latex =3{{x}^4}-2{{x}^2}+4$
Obtuvimos exactamente la misma función que $latex f(x)$. Entonces, la función sí tiene simetría con respecto al eje y.
Prueba 2: Ahora, buscamos simetría con respecto al origen. Ncesitamos reemplazar tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$.
$latex -f(-x)=3{{(-x)}^4}-2{{(-x)}^2}+4$
$latex -f(-x)=3{{x}^4}-2{{x}^2}+4$
$latex f(-x)=-3{{x}^4}+2{{x}^2}-4$
Luego de multiplicar por -1, no obtuvimos la función original. Entonces, la función no es simétrica con respecto al origen.
EJERCICIO 5
¿Es la función $latex f(x)={{x}^3}+{{x}^2}+x+1$ simétrica con respecto al eje y o el origen?
Solución
Prueba 1: Verificamos simetría con respecto al eje y al reemplazar todas las x con –x:
$$f(-x)={{(-x)}^3}+{{(-x)}^2}+(-x)+1$$
$latex =-{{x}^3}+{{x}^2}-x+5$
Vemos que no obtuvimos la misma función que la función original, $latex f(x)$, lo que significa que la función no es simétrica con respecto al eje y.
Prueba 2: Podemos verificar si la función tiene simetría con respecto al original reemplazar tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$.
$$-f(-x)={{(-x)}^3}+{{(-x)}^2}+(-x)+1$$
$latex -f(-x)=-{{x}^3}+{{x}^2}-x+5$
$latex f(-x)={{x}^3}-{{x}^2}+x-5$
Luego de simplificar y multiplicar a la función por -1, no obtuvimos la función original, lo que significa que no es simétrica con respecto al origen.
Esta función no tiene ningún tipo de simetría. Esto no es inusual, ya que la mayoría de funciones no tienen ningún tipo de simetría.
EJERCICIO 6
Determina si la función $latex f(x)=3{{x}^5}-4{{x}^3}+2x+4$ tiene algún tipo de simetría.
Solución
Prueba 1: Reemplazamos todas las x con –x para buscar simetría con respecto al eje y:
$$f(-x)=3{{(-x)}^5}-4{{(-x)}^3}+2(-x)+4$$
$latex =-3{{x}^5}+4{{x}^3}-2x+4$
Después de simplificar, no obtuvimos la función original, lo que significa que ambas no son equivalentes y no existe simetría con respecto al eje y.
Prueba 2: Reemplazamos tanto a x con –x como a $latex f(x)$ con $latex -f(-x)$ para buscar simetría con respecto al origen:
$$-f(-x)=3{{(-x)}^5}-4{{(-x)}^3}+2(-x)+4$$
$latex -f(-x)=-3{{x}^5}+4{{x}^3}-2x+4$
$latex f(-x)=3{{x}^5}-4{{x}^3}+2x-4$
No obtuvimos exactamente la función original, por lo que la función no es simétrica con respecto al origen.
Ejercicios de simetría de funciones para resolver
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas: