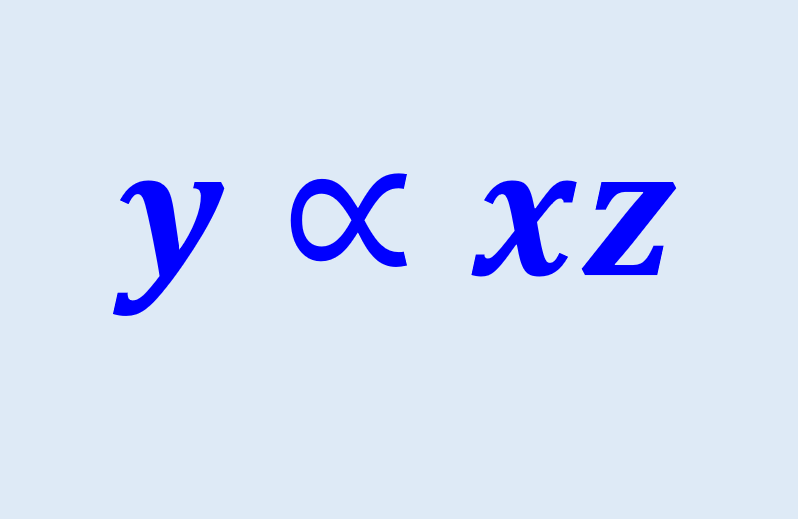La proporcionalidad nos permite relacionar dos o más cantidades. En el caso de la proporcionalidad compuesta, estamos relacionando a tres cantidades al mismo tiempo. La proporcionalidad compuesta es representada como y∝xz. Si es que usamos la constante k, podemos formar la ecuación y=kxz.
A continuación, veremos un resumen breve sobre cómo resolver ejercicios de proporcionalidad compuesta. Además, exploraremos varios ejercicios resueltos para entender la aplicación del proceso.
Resumen de proporcionalidad compuesta
Podemos resolver problemas de proporcionalidad compuesta siguiendo los siguientes pasos:
Paso 1: Escribimos la ecuación correcta. Los problemas de proporcionalidad compuesta son resueltos usando la ecuación $latex y=kxz$. Las variables y, x y z pueden ser cambiadas para usar variables que sean más relevantes para ciertos problemas verbales.
Además, debemos analizar el problema detenidamente para determinar si tenemos que modificar la ecuación de proporcionalidad compuesta al incluir cuadrados, cubos o raíces cuadradas.
Paso 2: Usamos la información dada en el problema para encontrar el valor de k, denominada la constante de proporcionalidad.
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos el valor de k encontrado en el paso 2.
Paso 4: Usamos la ecuación encontrada en el paso 3 y el resto de información dada en el problema para encontrar la respuesta al problema.
Ejercicios de proporcionalidad compuesta resueltos
Usa los siguientes ejercicios de proporcionalidad compuesta para estudiar detalladamente el uso de los pasos mencionados arriba. Cada uno de los ejercicios tiene una solución detallada que facilita el entendimiento.
EJERCICIO 1
Si es que y varía conjuntamente con x y z, y si es que tenemos que $latex y=24$ cuando $latex x=18$ y $latex z=6$, encuentra z cuando $latex y=12$ y $latex x=30$.
Solución
Paso 1: Escribimos la ecuación correcta:
$latex y=kxz$
Paso 2: Usamos la información dada en el problema para encontrar el valor de k. En este caso, tenemos $latex y=24$, $latex x=18$ y $latex z=6$:
$latex 24=k(18)(6)$
$latex 24=108k$
$latex \frac{2}{9}=k$
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos $latex k=\frac{2}{9}$:
$latex y=\frac{2}{9}xz$
Paso 4: Usamos la ecuación encontrada en el paso 3 y reemplazamos $latex y=12$ y $latex x=30$:
$latex 12=\frac{2}{9}(30)z$
$latex 12=\frac{20}{3}z$
$latex 36=20z$
$latex \frac{9}{5}=z$
EJERCICIO 2
Si es que a varía conjuntamente con b y c cuadrado y tenemos que $latex a=225$ cuando $latex b=4$ y $latex c=3$, encuentra el valor de a cuando $latex b=6$ y $latex c=8$.
Solución
Paso 1: Escribimos la ecuación correcta. En este caso, usamos las variables a, b y c y elevamos a c al cuadrado:
$latex a=kb{{c}^2}$
Paso 2: Usamos la información dada en el problema para encontrar el valor de k. En este caso, tenemos $latex a=225$, $latex b=4$ y $latex c=3$:
$latex 225=k(4)({{3}^2})$
$latex 225=36k$
$latex \frac{25}{4}=k$
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos $latex k=\frac{25}{4}$:
$latex a=\frac{25}{4}b{{c}^2}$
Paso 4: Usamos la ecuación encontrada en el paso 3 y reemplazamos $latex b=6$ y $latex c=8$:
$latex a=\frac{25}{4}(6)({{8}^2})$
$latex a=2400$
EJERCICIO 3
Si es que m varía conjuntamente con n cubo y o y si es que tenemos que $latex m=24$ cuando $latex n=8$ y $latex o=6$, encuentra el valor de $latex m$ cuando $latex n=4$ y $latex o=12$.
Solución
Paso 1: Escribimos la ecuación correcta. En este caso, tenemos las variables m, n y o y tenemos la variable n elevada al cubo.
$latex m=k{{n}^3}o$
Paso 2: Usamos la información dada en el problema para encontrar el valor de k. En este caso, tenemos $latex m=24$, $latex n=8$ y $latex o=6$:
$latex 24=k(8)(6)$
$latex 24=48k$
$latex \frac{1}{2}=k$
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos $latex k=\frac{1}{2}$:
$latex m=\frac{1}{2}{{n}^3}o$
Paso 4: Usamos la ecuación encontrada en el paso 3 y reemplazamos $latex n=4$ y $latex o=12$:
$latex m=\frac{1}{2}({{4}^3})(12)$
$latex m=384$
EJERCICIO 4
El volumen de un cono varía conjuntamente con su altura y el cuadrado de su radio. Un cono con un radio de 4 metros y una altura de 9 metros tiene un volumen de 48π metros cúbicos.
Encuentra el volumen de un cubo que tiene un radio de 8 metros y una altura de 6 metros.
Solución
Paso 1: Escribimos la ecuación correcta. En este caso, vamos a usar las variables v, h y r para representar al volumen, a la altura y al radio respectivamente:
$latex v=kh{{r}^2}$
Paso 2: Usamos la información dada en el problema para encontrar el valor de k. En este caso, tenemos $latex v=48\pi$, $latex h=9$ y $latex r=4$:
$latex 48\pi=k(9)({{4}^2})$
$latex 48\pi=144k$
$latex \frac{\pi}{3}=k$
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos $latex k=\frac{\pi}{3}$:
$latex v=\frac{\pi}{3}h{{r}^2}$
Paso 4: Usamos la ecuación encontrada en el paso 3 y reemplazamos $latex r=8$ y $latex h=6$:
$latex v=\frac{\pi}{3}(6)({{8}^2})$
$latex v=128\pi$
EJERCICIO 5
La energía cinética varía conjuntamente con la masa y el cuadrado de la velocidad. Una masa de 6 kilogramos y una velocidad de 10 metros por segundo tiene una energía cinética de 300 Julios.
Encuentra la energía cinética para una masa de 5 kilogramos y una velocidad de 6 metros por segundo.
Solución
Paso 1: Escribimos la ecuación correcta. Aquí, vamos a usar las variables e, m y v para representar a la energía, a la masa y a la velocidad respectivamente:
$latex e=km{{v}^2}$
Paso 2: Usamos la información dada en el problema para encontrar el valor de k. En este caso, tenemos $latex e=300$, $latex m=6$ y $latex v=10$:
$latex 300=k(6)(10)$
$latex 300=600k$
$latex \frac{1}{2}=k$
Paso 3: Reescribimos la ecuación del paso 1 y sustituimos $latex k=\frac{1}{2}$:
$latex e=\frac{1}{2}m{{v}^2}$
Paso 4: Usamos la ecuación encontrada en el paso 3 y reemplazamos $latex m=5$ y $latex v=6$:
$latex e=\frac{1}{2}(5)({{6}^2})$
$latex e=90$
Ejercicios de proporcionalidad compuesta para resolver
Usa los siguientes ejercicios para poner a prueba tus habilidades y tu entendimiento de proporcionalidad compuesta. Selecciona una respuesta y verifícala para saber si escogiste la respuesta correcta.
Mira los ejercicios resueltos de arriba si es que tienes problemas con este tema.
Véase también
¿Interesado en aprender más sobre proporcionalidad? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
