El dominio puede ser calculado al encontrar el conjunto de todos los valores posibles para la variable independiente, generalmente la x. El rango puede ser calculado al encontrar el conjunto de todos los valores posibles para la variable dependiente, generalmente la y.
A continuación, miraremos un resumen del dominio y el rango de una función. Revisaremos cómo encontrar el dominio y el rango. Además, resolveremos varios ejercicios de dominio y rango para aprender el razonamiento usado al momento de resolver este tipo de ejercicios.
Resumen de dominio y rango
Dominio
El dominio de una función es el conjunto de todos los valores posibles de la variable independiente. Es decir, el dominio es el conjunto de todos los valores de x que harán que la función produzca valores reales de y.
Para encontrar el dominio de una función, recordamos lo siguiente:
- El denominador de una fracción no puede ser igual a cero.
- El número debajo de un signo de raíz cuadrada no puede ser negativo
Entonces, el dominio de una función es encontrado al buscar los valores de la variable independiente (usualmente x) que sí podemos usar. Tenemos que evitar el 0 en el denominador de una fracción y números negativos en raíces cuadradas.
Rango
El rango de una función es el conjunto de todos los valores posibles de la variable dependiente (usualmente la y) después de haber usado el dominio. Esto significa que el rango es el conjunto de los valores de y que obtenemos después de usar todos los valores de x.
Para encontrar el rango de una función, consideramos lo siguiente:
- El rango es la extensión de los valores de y, desde el valor mínimo al valor máximo.
- Podemos sustituir valores de x para analizar el resultado, considerando si es que los valores son negativos o positivos.
- Tenemos que asegurarnos de buscar valores máximos y mínimos.
Ejercicios de dominio y rango resueltos
Los siguientes ejercicios de dominio y rango tienen su respectiva solución. Cada solución detalla el proceso y el razonamiento usados para obtener la respuesta.
EJERCICIO 1
Encuentra el dominio y el rango de la función $latex f(x)={{x}^2}+1$.
Solución
Dominio: La función $latex f(x)={{x}^2}+1$ está definida para todos los valores reales de x ya que no hay restricciones en el valor de x. Entonces, el dominio de x es:
“Todos los valores reales de x“
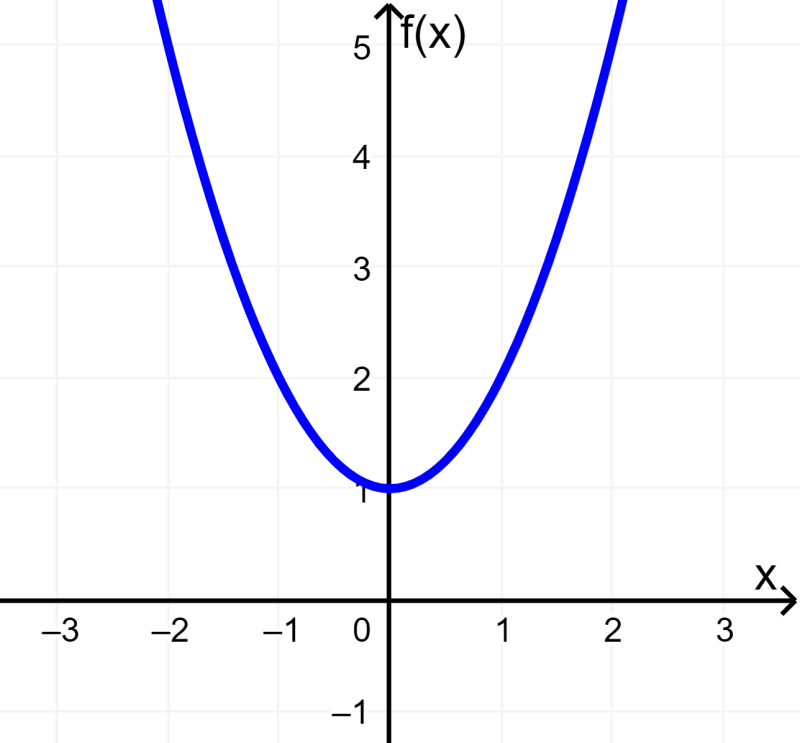
Rango: Dado que $latex {{x}^2}$ nunca es negativo, $latex {{x}^2}+1$ nunca es menor que 1. Entonces, el rango de $latex f(x)$ es:
“Todos los números reales $latex f(x) \geq 1$”
Podemos ver que x puede tomar cualquier valor en la gráfica, pero los valores de $latex y=f(x)$ son mayores o iguales a 1.
EJERCICIO 2
Encuentra el dominio y el rango de la función $latex f(x)= \frac{1}{x+3}$.
Solución
Dominio: La función $latex f(x)= \frac{1}{x+3}$ no está definida para $latex x=-3$ ya que esto produciría una división por cero (tendríamos un 0 en el denominador). Entonces, el dominio de $latex f(x)$ es:
“Todos los números reales excepto el -3”
Rango: Sin importar qué tan grande o pequeño sea x, los valores de $latex f(x)$ nunca serán iguales a cero. Si es que intentamos resolver la ecuación para 0, tenemos:
$latex 0= \frac{1}{x+3}$
Multiplicando ambos lados por $latex x+3$, tenemos:
$latex 0= 1$
Esto es imposible. Entonces, el rango de $latex f(x)$ es:
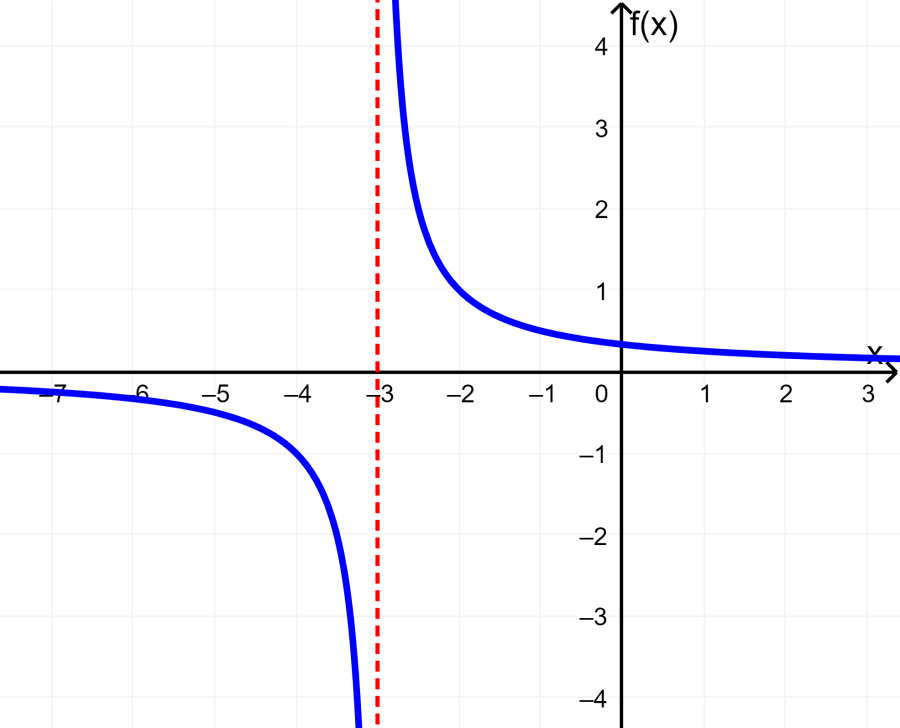
“Todos los números reales excepto el cero”
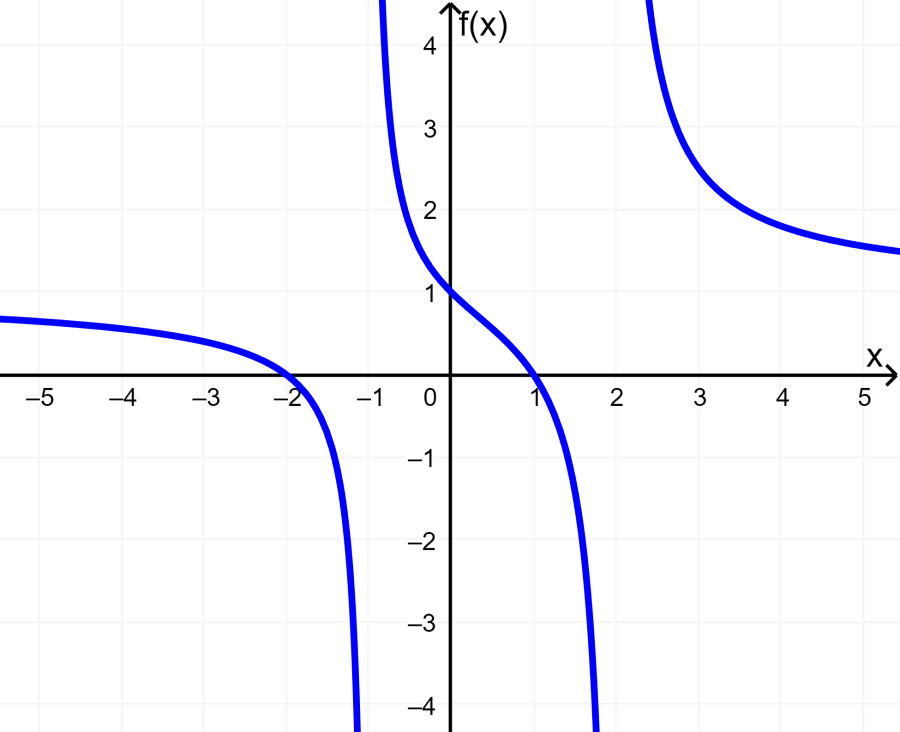
En la gráfica, podemos ver que la función no está definida para $latex x=-3$ y que la función toma todos los valores de y a excepción del cero:
EJERCICIO 3
Encuentra el dominio y el rango de la función $latex f(t)=\sqrt{5-t}$.
Solución
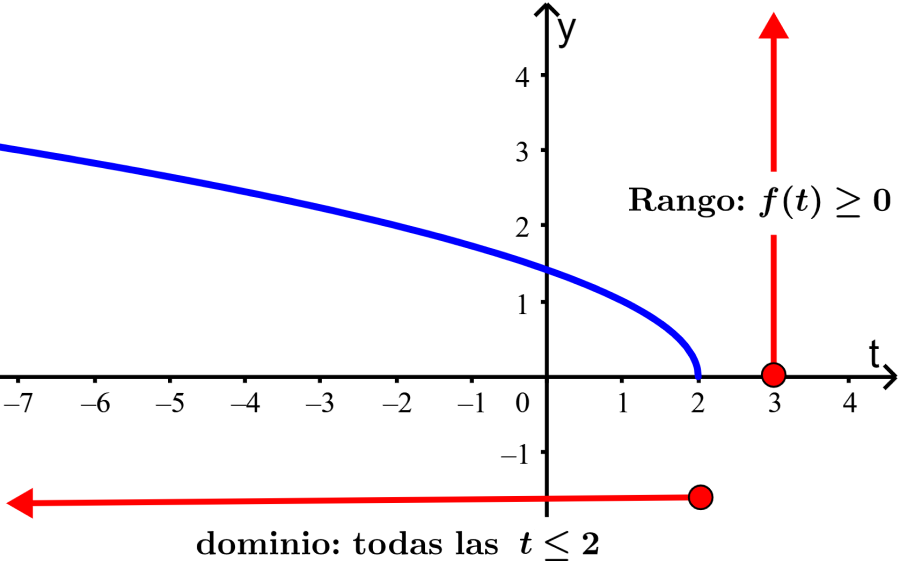
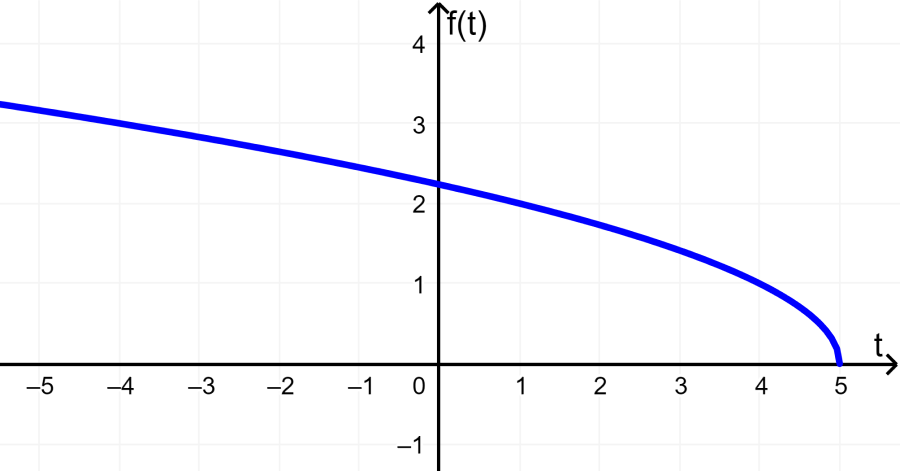
Dominio: La función $latex f(t)=\sqrt{5-t}$ no está definida para los números reales mayores que 5, ya que esto resultaría en números negativos debajo de la raíz cuadrada y números imaginarios para $latex f(t)$, entonces, el dominio de $latex f(t)$ es:
“Todos los números reales, $latex t\leq 5$”
Rango: Por definición de una raíz cuadrada tenemos:
$latex f(t)=\sqrt{5-t}\geq 0$
Entonces, el rango de $latex f(t)$ es:
“Todos los números reales, $latex f(t)\geq 0$”
En la gráfica, podemos ver que $latex t$ no toma valores mayores que 5 y que el rango es mayor o igual a 0:
EJERCICIO 4
Determina el dominio y el rango de la función $latex f(x)=\frac{{{x}^2}+x-2}{{{x}^2}-x-2}$.
Solución
Dominio: El único problema que tenemos en esta función es que tenemos que ser cuidadosos para no dividir por cero. Entonces los valores de x no puede tomar aquellos valores que produzcan una división por cero. Entonces, hacemos que el denominador sea igual a cero y resolvemos:
$latex {{x}^2}-x-2=0$
$latex (x+1)(x-2)=0$
$latex x=-1$ o $latex x=2$
Entonces, el dominio es:
“Todos los números reales excepto el -1 y el 2”
Rango: El rango es un poco más difícil de determinar, pero en este caso, no tenemos restricciones visibles que hagan que el rango sea mayor o menor que un valor específico. Comprobamos esto con la gráfica de la función:
Vemos que la función toma todos los valores de y, por lo que el rango es:
“Todos los números reales”
EJERCICIO 5
Determina el dominio y el rango de la función $latex g(x)=-\sqrt{-2x+5}$.
Solución
Dominio: El único problema que tenemos en esta función es que no podemos tener valores negativos dentro del signo de raíz cuadrada. Entonces, podemos hacer que la expresión dentro de la raíz cuadrada sea mayor que o igual a cero y resolvemos:
$latex -2x+5\geq 0$
$latex -2x\geq -5$
$latex 2x\leq 5$
$latex x\leq \frac{5}{2}$
Entonces, el dominio es:
“Todos los números reales $latex x\leq \frac{5}{2}$”
Rango: Sabemos que por definición, el resultado de una raíz cuadrada debe ser mayor o igual que cero. Sin embargo, en este caso, tenemos un signo negativo que precede a la raíz cuadrada, por lo que el rango es:
“Todos los números reales $latex g(x)\leq 0$”
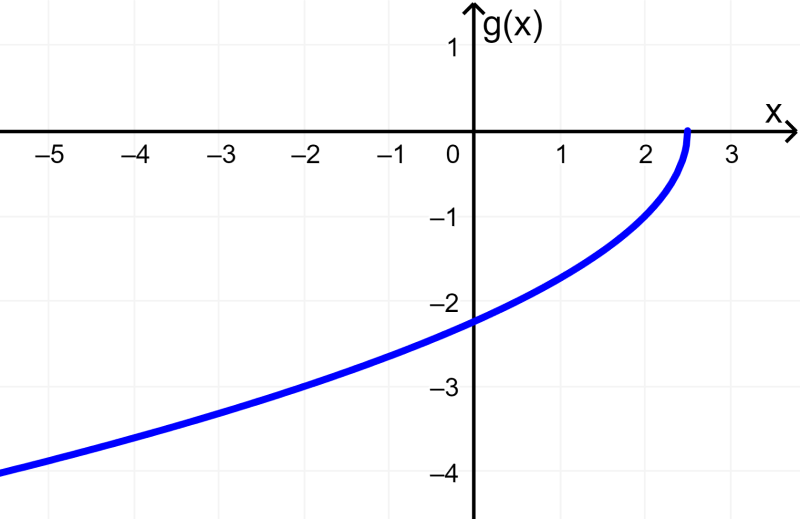
Podemos mirar la gráfica para comprobar esto:
EJERCICIO 6
Encuentra el dominio y el rango de la función $latex f(x)=-{{x}^4}+2$.
Solución
Dominio: Este es un problema fácil. No hay denominadores, por lo que no tenemos problemas de división por cero y no hay radicales, por lo que no tenemos problemas con números negativos en raíces cuadradas. Cuando tenemos un polinomio como en este caso, el dominio es:
“Todos los números reales”
Rango: El rango varía de polinomio a polinomio. En este caso, sabemos que $latex {{x}^4}$ siempre es positivo, por lo que al ser precedido por un signo negativo, siempre obtenemos un número negativo o igual a 0. Eso significa que el punto más alto es 2 y el rango es:
Todos los números reales, $latex f(x)\leq 2$”
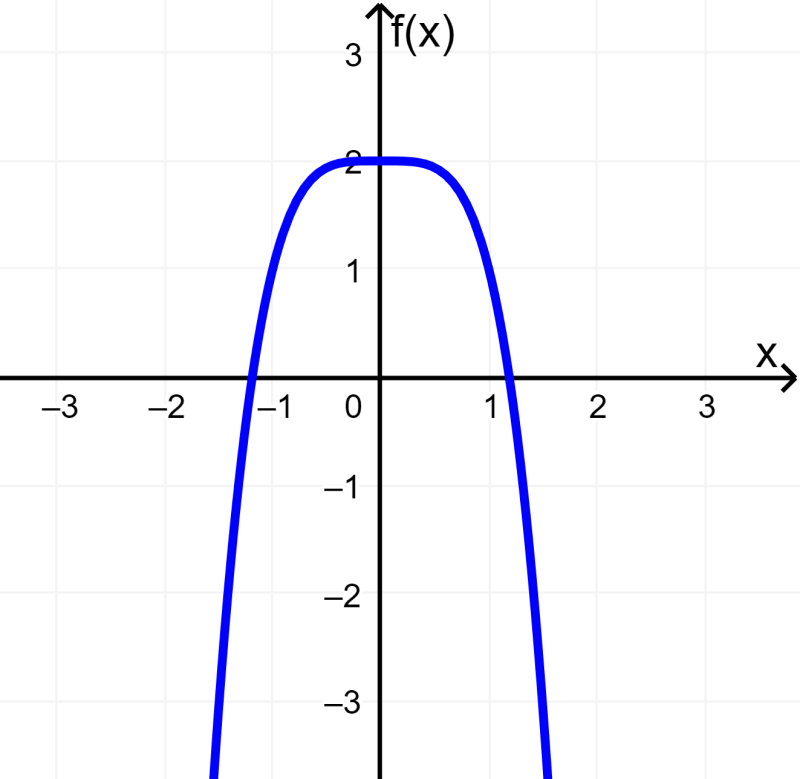
En la gráfica, podemos ver esto:
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
