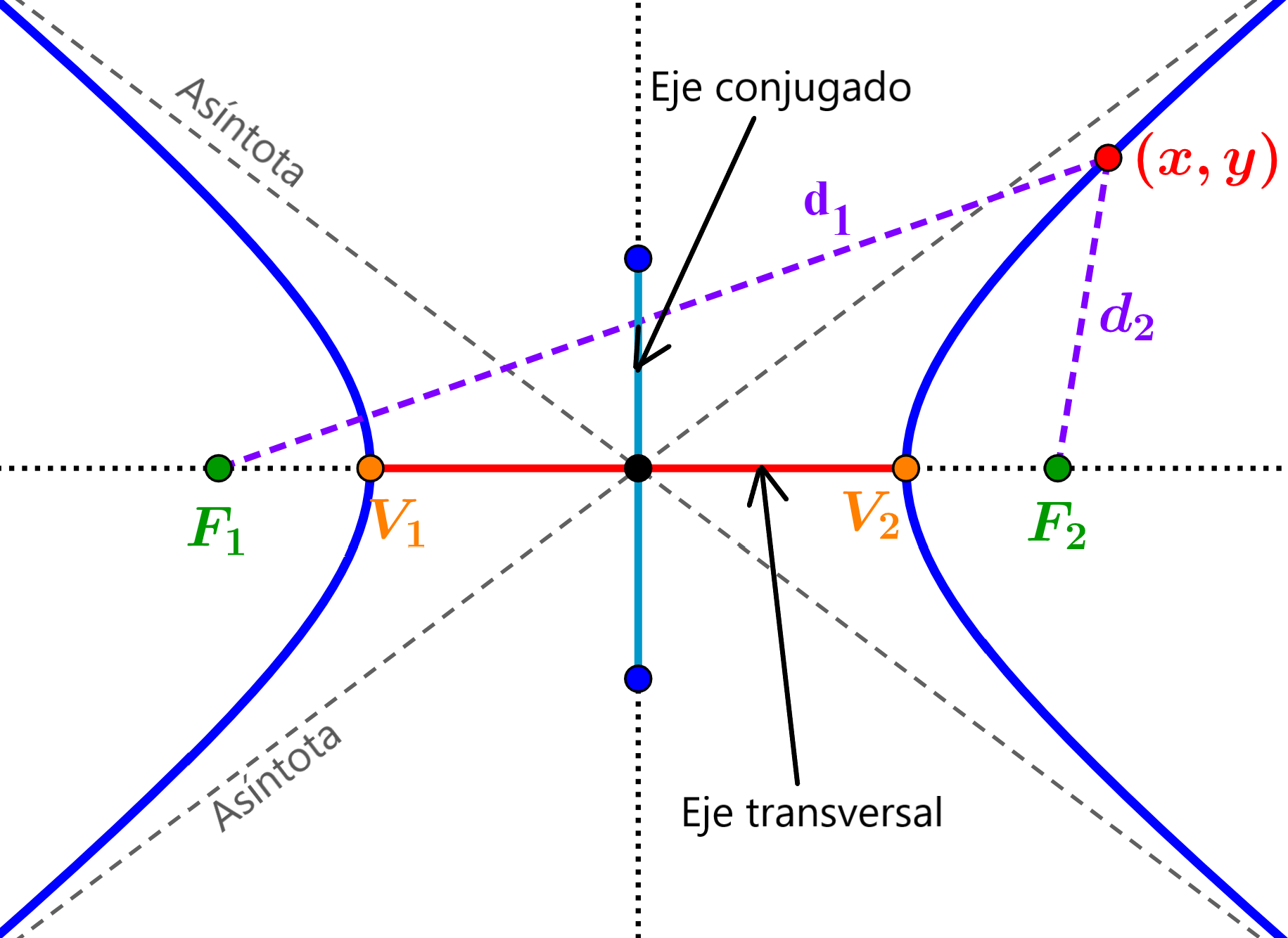
Las hipérbolas son formadas por el conjunto de todos los puntos en el plano cartesiano de modo que la diferencia de las distancias entre cualquier punto y los focos es igual a una constante. Las hipérbolas tienen dos ejes de simetría. El eje transversal es definido como el segmento que une a los dos vértices y que pasa por el centro. El eje conjugado es el segmento que conecta a los dos cóvertices y que es perpendicular al eje transversal. Los focos se ubican en la línea que contiene al eje transversal. El centro de la hipérbola está ubicado en el punto de intersección del eje transversal y el eje conjugado. Las dos asíntotas de la hipérbola también intersecan en el centro.
Existen cuatro variaciones de la ecuación de una hipérbola. Primeramente, tenemos dos variaciones dependiendo en la ubicación del centro. El centro puede estar ubicado en el origen o fuera del origen. También, tenemos dos variaciones dependiendo en si la hipérbola está orientada horizontalmente o verticalmente.
Ecuación de hipérbolas centradas en el origen
La ecuación de una hipérbola que tiene al centro en el origen tiene dos variaciones que dependen de su orientación. Cuando el eje transversal (segmento que conecta a los vértices) de la hipérbola está ubicado en el eje x, la hipérbola está orientada horizontalmente.
Cuando el eje transversal está ubicado en el eje y, la hipérbola está orientada verticalmente.
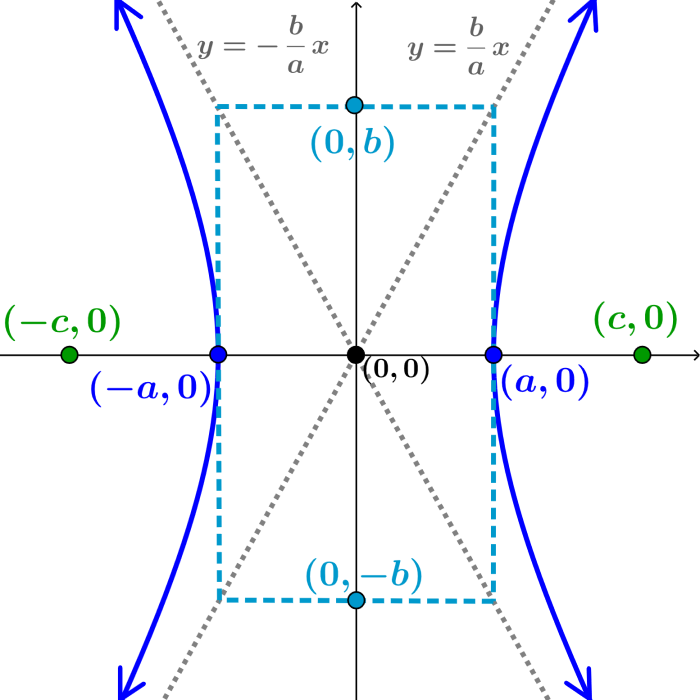
Hipérbola orientada horizontalmente
Cuando la hipérbola está centrada en el origen, (0, 0) y su eje transversal está en el eje x, su ecuación en forma estándar es:
| $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$ |
en donde,
- La longitud del eje transversal es $2a$
- Los vértices tienen las coordenadas $latex (\pm a, 0)$
- El eje conjugado (segmento que une a los covértices) tiene una longitud de $latex 2b$
- Los covértices tienen las coordenadas $latex (0, \pm b)$
- La distancia entre los focos es $latex 2c$, en donde, $latex {{c}^2}={{a}^2}+{{b}^2}$
- Los focos tienen las coordenadas $latex (\pm c, 0)$
- Las asíntotas tienen las ecuaciones $latex y=\pm \frac{b}{a}x$
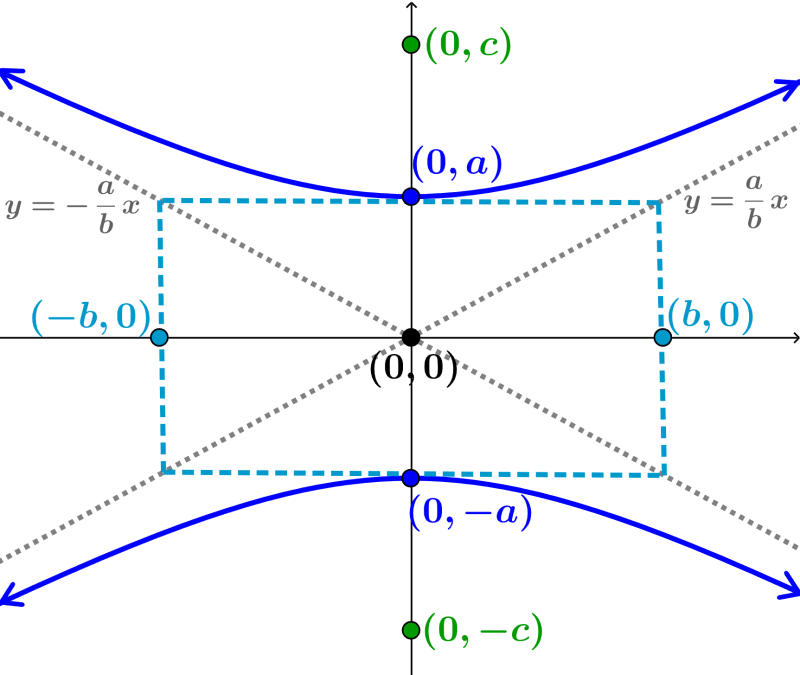
Hipérbola orientada verticalmente
Una hipérbola que está centrada en el origen, (0, 0), y que tiene a su eje transversal en el eje y, tiene la ecuación general:
| $latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$ |
en donde,
- $2a$ representa a la longitud del eje transversal
- Los vértices están ubicados en $latex (0, \pm a)$
- $latex 2b$ representa a la longitud del eje conjugado
- Los covértices están ubicados en $latex (\pm b, 0)$
- $latex 2c$ representa a la distancia entre los focos, en donde, $latex {{c}^2}={{a}^2}+{{b}^2}$
- Los focos están ubicados en $latex (0, \pm c)$
- Las ecuaciones de las asíntotas son $latex y=\pm \frac{a}{b}x$
Usar los vértices y los focos para encontrar ecuaciones de hipérbolas centradas en el origen
Cuando una hipérbola está centrada en el origen, podemos usar las coordenadas de los vértices y los focos junto con los siguientes pasos para encontrar su ecuación:
Paso 1: Determinar la ubicación del eje transversal con respecto el eje x o en el eje y para conocer su orientación.
1.1. Una hipérbola está orientada horizontalmente cuando las coordenadas de los vértices tienen la forma $latex (\pm a, 0)$ y las coordenadas de los focos tienen la forma $latex (\pm c, 0)$. En este caso, usamos la forma $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$.
1.2. Una hipérbola está orientada verticalmente cuando las coordenadas de los vértices tienen la forma $latex (0, \pm a)$ y las coordenadas de los focos tienen la forma $latex (0, \pm c)$. En estos casos, tenemos la forma $latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$.
Paso 2: Encontramos el valor de $latex {{b}^2}$, usando la ecuación $latex {{b}^2}={{c}^2}-{{a}^2}$.
Paso 3: Reemplazamos los valores de $latex {{a}^2}$ y $latex {{b}^2}$ en la forma general del paso 1.
EJEMPLO
Si es que una hipérbola que tiene los vértices en $latex (\pm 5, 0)$ y los focos en $latex (\pm 6, 0)$, ¿cuál es su ecuación?
Solución
Mirando a las coordenadas de los focos y los vértices, concluimos que están ubicados en el eje x. Por lo tanto, sabemos que el eje transversal está en el eje x y la ecuación tendrá la siguiente forma:
$latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$
Usando los vértices $latex (\pm 5, 0 )$, obtenemos el valor $latex a=5$ y tenemos $latex {{a}^2}=25$.
Usando los focos $latex (\pm 6,0)$, obtenemos el valor $latex c=6$ y tenemos $latex {{c}^2}=36$.
Usando la ecuación $latex {{b}^2}={{c}^2}-{{a}^2}$, encontramos el valor de $latex {{b}^2}$:
$latex {{b}^2}={{c}^2}-{{a}^2}$
$latex {{b}^2}=36-25$
$latex {{b}^2}=11$
Al usar los valores encontramos, definimos a la ecuación de la hipérbola:
$latex \frac{{{x}^2}}{25}-\frac{{{y}^2}}{11}=1$
Ecuación de hipérbolas centradas fuera del origen
Podemos obtener la ecuación de hipérbolas centradas fuera del origen al aplicar una traslación a la ecuación general. Si es que trasladamos a la hipérbola h unidades en el eje x y k unidades en el eje y, el nuevo centro estará ubicado en $latex (h, k)$.
En este caso, la ecuación de la hipérbola también depende de su orientación.
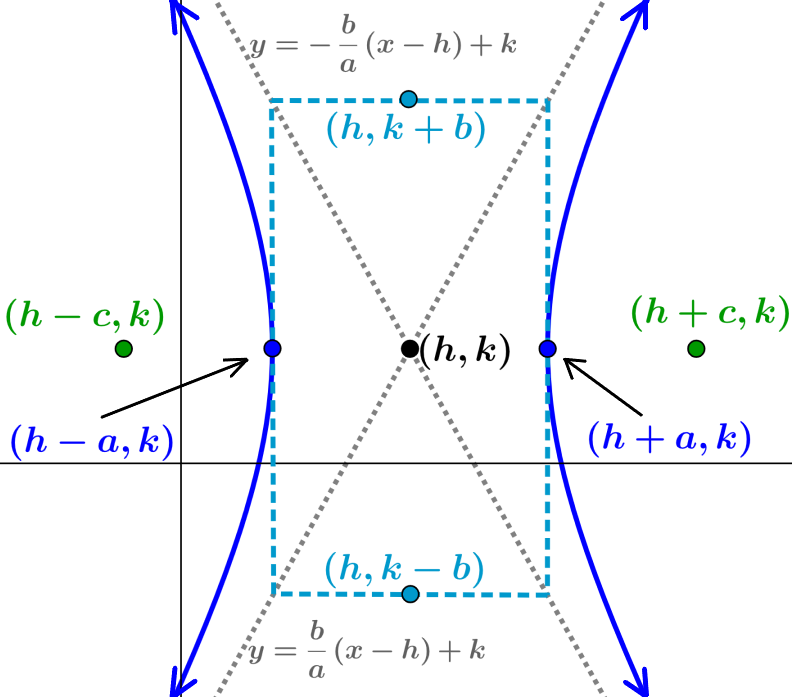
Hipérbola orientada horizontalmente con centro fuera del origen
Cuando la hipérbola tiene al centro en el punto $latex (h, k)$ y su eje transversal es paralelo al eje x, su ecuación es:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
en donde,
- h es el componente en x del centro y k es el componente en y del centro
- El eje transversal tiene una longitud de $latex 2a$
- Las coordenadas de los vértices son $latex (h\pm a, k)$
- El eje conjugado tiene una longitud de $latex 2b$
- Las coordenadas de los covértices son $latex (h, k\pm b)$
- La distancia entre los focos es $latex 2c$, en donde, $latex {{c}^2}={{a}^2}+{{b}^2}$
- Las coordenadas de los focos son $latex (h\pm c, 0)$
- Las asíntotas tienen las ecuaciones $latex y=\pm \frac{b}{a}(x-h)+k$
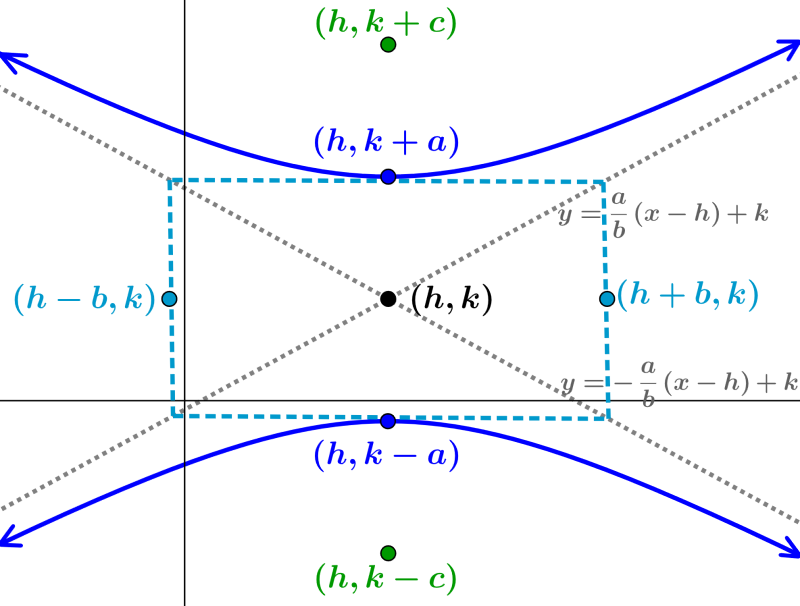
Hipérbola orientada verticalmente con centro fuera del origen
Si es que una hipérbola está centrada en $latex (h, k)$ y su eje transversal es paralelo al eje y, su ecuación es:
| $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$ |
en donde,
- h es el componente en x del centro y k es el componente en y del centro
- El eje transversal mide $latex 2a$
- Los vértices tienen las coordenadas $latex (h, k\pm a)$
- El eje conjugado mide $latex 2b$
- Los covértices tienen las coordenadas $latex (h\pm b, k)$
- La distancia entre los focos es $latex 2c$, en donde, $latex {{c}^2}={{a}^2}+{{b}^2}$
- Las coordenadas de los focos son $latex (h, k\pm c)$
- Las ecuaciones de las asíntotas son $latex y=\pm \frac{a}{b}(x-h)+k$
Usar los vértices y los focos para encontrar la ecuación de hipérbolas centradas fuera del origen
La ecuación de una hipérbola que está centrada fuera del origen puede ser encontrada usando los siguientes pasos:
Paso 1: Determinar si el eje transversal es paralelo al eje x o paralelo al eje y para conocer la orientación de la hipérbola.
1.1. Una hipérbola está orientada horizontalmente si es que las coordenadas en y de los vértices son las mismas que las coordenadas en y de los focos. En este caso, usamos la ecuación $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$.
1.2. Una hipérbola está orientada verticalmente si es que las coordenadas en x de los vértices son las mismas que las coordenadas en x de los focos. En este caso, usamos la ecuación $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$.
Paso 2: El centro de la hipérbola, $latex (h, k)$, es encontrado usando las coordenadas de los vértices y la fórmula del punto medio.
Paso 3: Encontramos a $latex {{a}^2}$ usando la distancia entre los vértices, $latex 2a$.
Paso 4: El valor de c es encontrado usando las coordenadas de los focos y los valores de h y k.
Paso 5: El valor de $latex {{b}^2}$ es encontrado usando la ecuación $latex {{b}^2}={{c}^2}-{{a}^2}$.
Paso 6: Usamos los valores de $latex {{a}^2}$ y $latex {{b}^2}$ en la ecuación general del paso 1.
EJEMPLO
¿Cuál es la ecuación de una hipérbola que tiene focos en (2, 0), (2, 6) y vértices en (2, 1), (2, 5)?
Solución
Observamos que las coordenadas en x de los focos y los vértices son las mismas, por lo que el eje transversal es paralelo al eje y. Esto significa que la ecuación de la hipérbola tiene la forma:
$latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$
Encontramos al centro usando la fórmula del punto medio y las coordenadas de los vértices (2, 1) y (2, 5):
$latex (h, k)=(\frac{2+2}{2}, \frac{1+5}{2})$
$latex =(2, 3)$
Encontramos el valor de $latex {{a}^2}$ usando la longitud del eje transversal, 2a. Por su parte, la longitud del eje transversal es igual a la diferencia en las coordenadas y de los vértices:
$latex 2a=|5-1|$
$latex 2a=4$
$latex a=2$
$latex {{a}^2}=4$
El valor de $latex {{c}^2}$ es encontrado usando las coordenadas de los focos, $latex (h, k\pm c)$. Podemos formar las ecuaciones $latex (h, k-c)=(2, 0)$ y $latex (h, k+c)=(2, 6)$. Ahora, usamos una de las ecuaciones para encontrar el valor de c:
$latex k+c=6$
$latex 3+c=6$
$latex c=3$
$latex {{c}^2}=9$
Usamos la ecuación $latex {{b}^2}={{c}^2}-{{a}^2}$ para encontrar el valor de $latex {{b}^2}$:
$latex {{b}^2}={{c}^2}-{{a}^2}$
$latex =9-4$
$latex =5$
Usando los valores de h, k, $latex {{a}^2}$ y $latex {{b}^2}$ en la forma general, tenemos:
$latex \frac{{{(y-3)}^2}}{4}-\frac{{{(y-2)}^2}}{5}=1$
Véase también
¿Interesado en aprender más sobre hipérbolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
