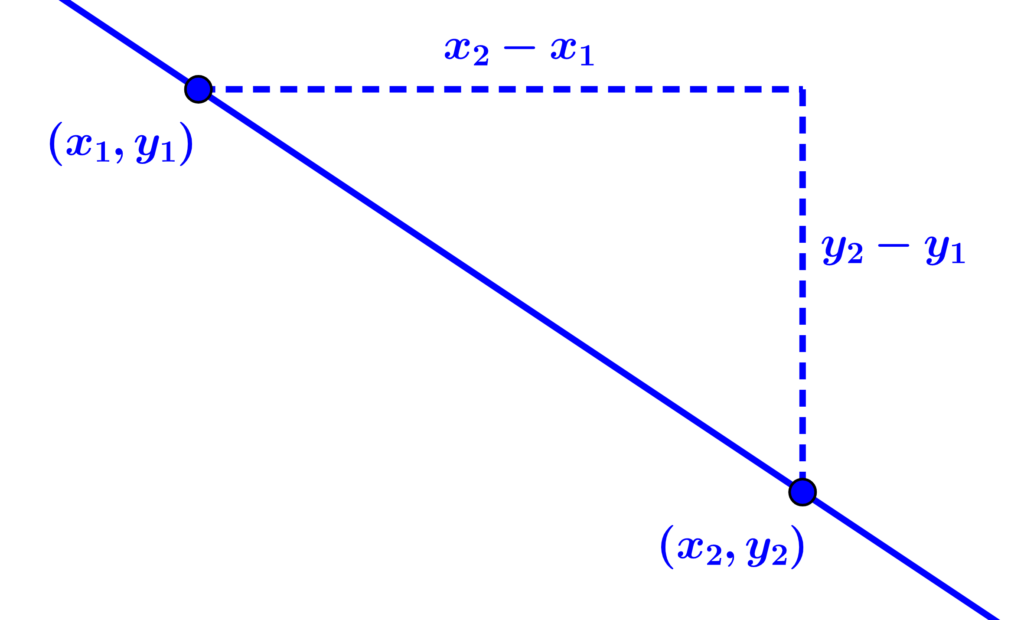
La ecuación de una línea es una ecuación que satisface y representa a cada uno de los puntos en la línea. La ecuación de una línea puede ser encontrada usando varios métodos dependiendo en la información que tengamos disponible.
En este artículo, aprenderemos sobre la ecuación de la recta punto pendiente. Miraremos varios ejercicios resueltos para conocer la aplicación de esta ecuación y entender completamente los conceptos.
¿Qué es la ecuación de la recta punto pendiente?
La fórmula de la ecuación de la recta punto pendiente es usada para encontrar la ecuación de una línea. Esta fórmula es usada solo cuando conocemos la pendiente de la recta y un punto por el que la recta pasa.
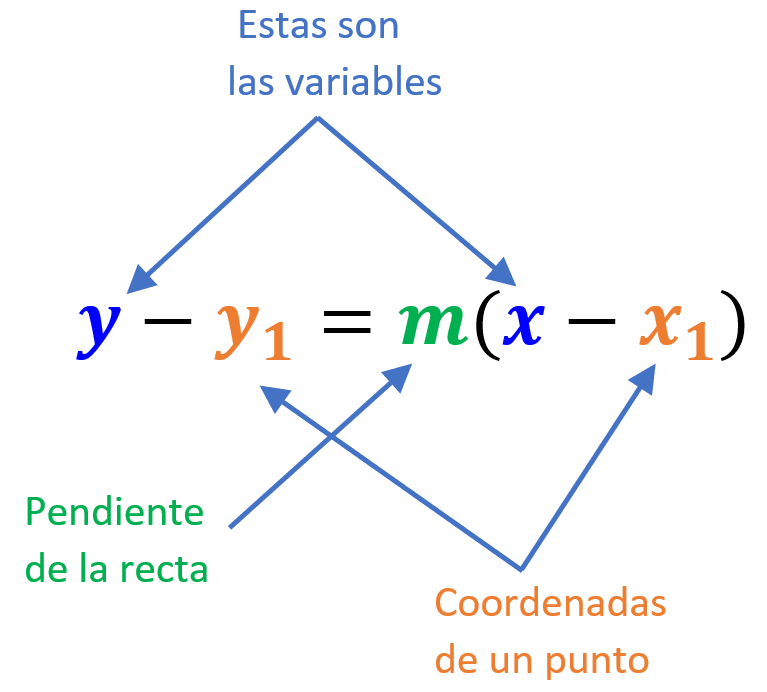
Entonces, la ecuación de una línea que tiene una pendiente m y la cual pasa por el punto $latex (x_{1}, ~y_{1})$ es encontrada usando esta forma. La ecuación de la forma punto pendiente es:
| $latex y-y_{1}=m(x-x_{1})$ |
en donde $latex (x_{1}, ~y_{1})$ es cualquier punto que se ubica en la línea.
Ecuación de la recta punto pendiente ejercicios resueltos
La forma punto pendiente es aplicada para encontrar la respuesta a los siguientes ejercicios. Estos ejercicios tienen una solución detallada que nos ayuda a entender el uso de la fórmula. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra la ecuación de la línea que pasa a través del punto (-3, 1) y tiene una pendiente de 2.
Solución
El punto dado que pasa por la recta es:
$latex (x_{1},~y_{1})=(-3, ~1)$
La pendiente de la línea es:
$latex m=2$
Encontramos la ecuación de la línea usando la fórmula punto pendiente:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=2(x-(-3))$
$latex y-1=2(x+3)$
$latex y-1=2x+6$
$latex y=2x+7$
Entonces, la ecuación de la recta es:
| $latex y=2x+7$ |
EJERCICIO 2
Encuentra la ecuación de la recta que tiene una pendiente de -1 y pasa a través del punto (2, 1).
Solución
El punto dado que pasa por la recta es:
$latex (x_{1},~y_{1})=(2, ~1)$
La pendiente de la recta es:
$latex m=-1$
Usamos la fórmula punto pendiente para encontrar la ecuación de la recta:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=-1(x-2)$
$latex y-1=-x+2$
$latex y=-x+3$
Entonces, la ecuación de la recta es:
| $latex y=-x+3$ |
EJERCICIO 3
Encuentra la ecuación de la línea que tiene una pendiente de $latex \frac{1}{2}$ y pasa a través del punto (-4, 3).
Solución
Tenemos que el siguiente punto pasa por la recta:
$latex (x_{1},~y_{1})=(-4, ~3)$
La pendiente de la línea es:
$latex m=\frac{1}{2}$
Usamos la fórmula punto pendiente para encontrar la ecuación de la línea:
$latex y-y_{1}=m(x-x_{1})$
$latex y-3=\frac{1}{2}(x-(-4))$
$latex y-3=\frac{1}{2}(x+4)$
$latex y-3=\frac{1}{2}x+2$
$latex y=\frac{1}{2}x+5$
Entonces, la ecuación de la recta es:
| $latex y=\frac{1}{2}x+5$ |
EJERCICIO 4
Encuentra la ecuación de la recta que pasa por el punto (3, 1) y tiene una pendiente de $latex -\frac{2}{3}$.
Solución
Tenemos que el siguiente punto pasa por la recta:
$latex (x_{1},~y_{1})=(3, ~1)$
La pendiente de la línea es:
$latex m=-\frac{2}{3}$
Encontramos la ecuación de la recta usando la forma punto pendiente:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=-\frac{2}{3}(x-3)$
$latex y-1=-\frac{2}{3}(x-2)$
$latex y-1=-\frac{2}{3}x+2$
$latex y=-\frac{2}{3}x+3$
Entonces, la ecuación de la recta es:
| $latex y=-\frac{2}{3}x+3$ |
EJERCICIO 5
Encuentra la ecuación de una línea horizontal que pasa por el punto (2,1).
Solución
Sabemos que la pendiente de una línea horizontal es $latex m=0$.
La línea pasa a través del punto $latex (x_{1}, ~y_{1})=(2, 1)$.
La ecuación de la línea usando la forma punto pendiente es:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=0(x-2)$
$latex y-1=0$
$latex y=1$
Entonces, la ecuaciónde la línea horizontal es:
| $latex y=1$ |
EJERCICIO 6
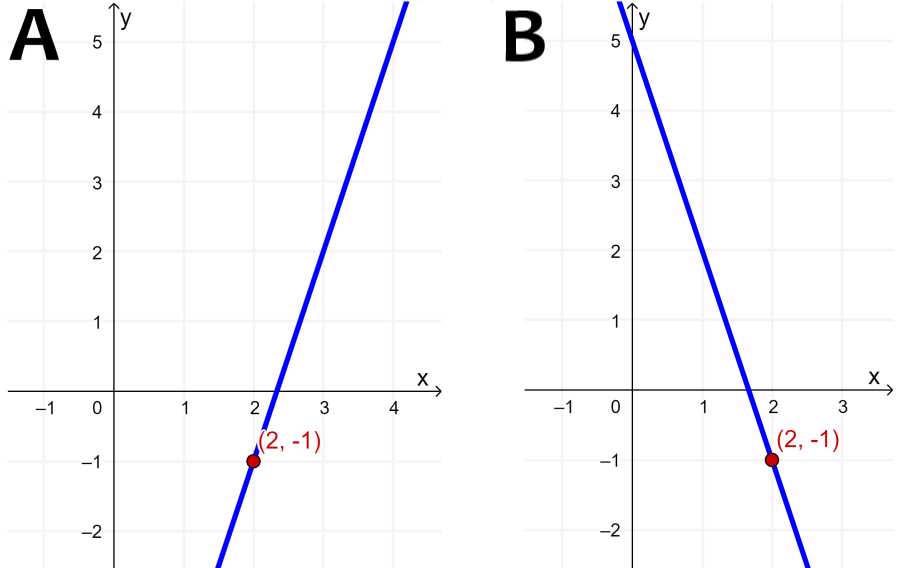
¿Cuál de las siguientes gráficas podría representar a la ecuación $latex y+1=-3(x-2)$?
Solución
Relacionando a la ecuación dada $latex y+1=-3(x-2)$ con la forma punto pendiente de una recta $latex y-y_{1}=m(x-x_{1})$, tenemos:
- $latex x_{1}=2$
- $latex y_{1}=-1$
- $latex m=-3$
Entonces, tenemos al punto $latex (x_{1}, ~y_{1})=(2, ~-1)$. Vemos que ambas gráficas contienen este punto, por lo que no hay ninguna diferencia ahí.
Sin embargo, tenemos la pendiente $latex m=-3$ y sabemos que una pendiente negativa tiene una inclinación hacia abajo, es decir, la recta decrece de izquierda a derecha. Esto significa que la gráfica B es la gráfica correcta de la ecuación.
Ejercicios de ecuación de la recta punto pendiente para resolver
Pon a prueba tu conocimiento sobre la forma punto pendiente de una recta con los siguientes ejercicios interactivos. Selecciona tu respuesta y verifícala para comprobar que escogiste la correcta.
Puedes mirar los ejercicios resueltos de arriba si tienes algún problema con estos ejercicios.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
