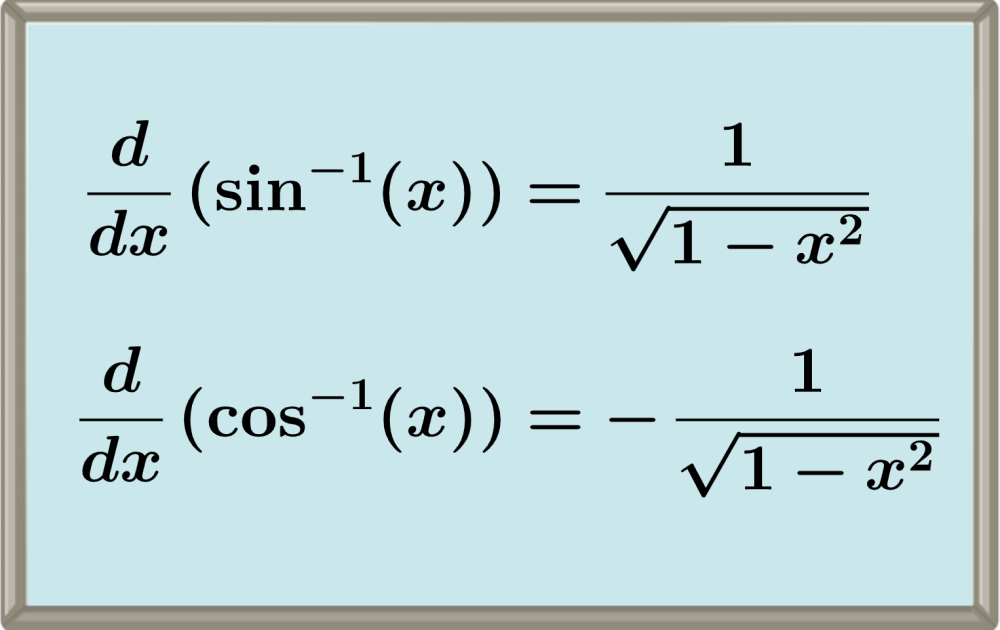Las funciones trigonométricas inversas son funciones que «revierten» el efecto causado por la función trigonométrica original. Las derivadas de estas funciones son obtenidas usando un triángulo rectángulo y el teorema de Pitágoras.
A continuación, conoceremos las fórmulas de las derivadas de las funciones trigonométricas inversas. Luego, aplicaremos estas fórmulas al resolver algunos ejercicios.
CÁLCULO
Relevante para…
Aprender sobre las derivadas de funciones trigonométricas inversas.
CÁLCULO
Relevante para…
Aprender sobre las derivadas de funciones trigonométricas inversas.
Fórmulas de las derivadas de funciones trigonométricas inversas
Derivada de la función seno inverso (arcsin)
La derivada de la función seno inverso estándar es:
$$\frac{d}{dx}(\sin^{-1}(x))=\frac{1}{\sqrt{1-x^2}}$$
Puedes explorar la demostración y versiones alternativas de la derivada del seno inverso en este artículo.
Derivada de la función coseno inverso (arccos)
La derivada de la función coseno inverso estándar es:
$$\frac{d}{dx}(\cos^{-1}(x))=-\frac{1}{\sqrt{1-x^2}}$$
Puedes explorar la demostración y versiones alternativas de la derivada del coseno inverso en este artículo.
Derivada de la función tangente inversa (arctan)
La derivada de la función tangente inversa estándar es:
$$\frac{d}{dx}(\tan^{-1}(x))=\frac{1}{1+x^2}$$
Puedes explorar la demostración y versiones alternativas de la derivada de la tangente inversa en este artículo.
Derivada de la función cosecante inversa (arccsc)
La derivada de la función cosecante inversa estándar es:
$$\frac{d}{dx}(\csc^{-1}(x))=-\frac{1}{|x|\sqrt{x^2-1}}$$
Puedes explorar la demostración y versiones alternativas de la derivada de la cosecante inversa en este artículo.
Derivada de la función secante inversa (arcsec)
La derivada de la función secante inversa estándar es:
$$\frac{d}{dx}(\sec^{-1}(x))=\frac{1}{|x|\sqrt{x^2-1}}$$
Puedes explorar la demostración y versiones alternativas de la derivada de la secante inversa en este artículo.
Derivada de la función cotangente inversa (arccot)
La derivada de la función cotangente inversa estándar es:
$$\frac{d}{dx}(\cot^{-1}(x))=-\frac{1}{1+x^2}$$
Puedes explorar la demostración y versiones alternativas de la derivada de la cotangente inversa en este artículo.
Ejercicios resueltos de derivadas de funciones trigonométricas inversas
EJERCICIO 1
Encuentra la derivada de la siguiente función:
$latex f(x)=\cos^{-1}(5x^2+10)$
Solución
Para derivar esta función, usamos la regla de la cadena con $latex y=\cos^{-1}(u)$ y con $latex u=5x^2+10$.
Entonces, con la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-u^2}}(10x)$$
Sustituyendo $latex u=5x^2+1$, tenemos:
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-(5x^2+10)^2}}(10x)$$
$$\frac{dy}{dx}=-\frac{10x}{\sqrt{1-(5x^2+10)^2}}$$
EJERCICIO 2
Deriva la siguiente función:
$latex f(x)=\sin^{-1}(4x^2+8)$
Solución
Esta es una función seno inversa compuesta. Entonces, usamos la regla de la cadena con $latex y=\sin^{-1}(u)$ y con $latex u=4x^2+8$.
Por la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{\sqrt{1-u^2}}(8x)$$
Sustituyendo $latex u=4x^2+8$, tenemos:
$$\frac{dy}{dx}=\frac{1}{\sqrt{1-(4x^2+8)^2}}(8x)$$
$$\frac{dy}{dx}=\frac{8x}{\sqrt{1-(4x^2+8)^2}}$$
EJERCICIO 3
Encuentra la derivada de la siguiente función:
$latex f(x)=\tan^{-1}(2x^3+2)$
Solución
En este caso, usamos la regla de la cadena con $latex y=\tan^{-1}(u)$ y con $latex u=2x^3+2$.
Por la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{ 1+u^2}(6x^2)$$
Sustituyendo $latex u=2x^3+2$, tenemos:
$$\frac{dy}{dx}=\frac{1}{1+(2x^3+2)^2}(6x^2)$$
$$\frac{dy}{dx}=\frac{6x^2}{1+(2x^3+2)^2}$$
EJERCICIO 4
Encuentra la derivada de la siguiente función:
$latex f(x)=\sec^{-1}(8x^2+4)$
Solución
Vamos a usar la regla de la cadena con $latex y=\sec^{-1}(u)$ y con $latex u=8x^2+4$.
Entonces, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{ |u|\sqrt{u^2-1}}(16x)$$
Sustituyendo $latex u=8x^2+4$, tenemos:
$$\frac{dy}{dx}=\frac{1}{ |8x^2+4|\sqrt{(8x^2+4)^2-1}}(16x)$$
$$\frac{dy}{dx}=\frac{16x}{ 4(2x^2+1)\sqrt{(8x^2+4)^2-1}}$$
$$\frac{dy}{dx}=\frac{4x}{ (2x^2+1)\sqrt{(8x^2+4)^2-1}}$$
Derivadas de funciones trigonométricas inversas – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre derivadas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
