La regla de la potencia es una de las reglas derivadas más utilizadas en Cálculo Diferencial (o Cálculo I) para derivar una variable elevada a un exponente numérico. Es una de las reglas de derivadas más sencillas que aprenden los estudiantes en los primeros capítulos de Cálculo diferencial.
Aunque se considera una de las reglas de derivadas más simples, es muy importante aprender cómo demostrar esta regla. Por lo tanto, en este artículo nos centraremos principalmente en las demostraciones de la fórmula de la regla de la potencia aplicando los principios del teorema del binomio y la diferenciación logarítmica.
CÁLCULO
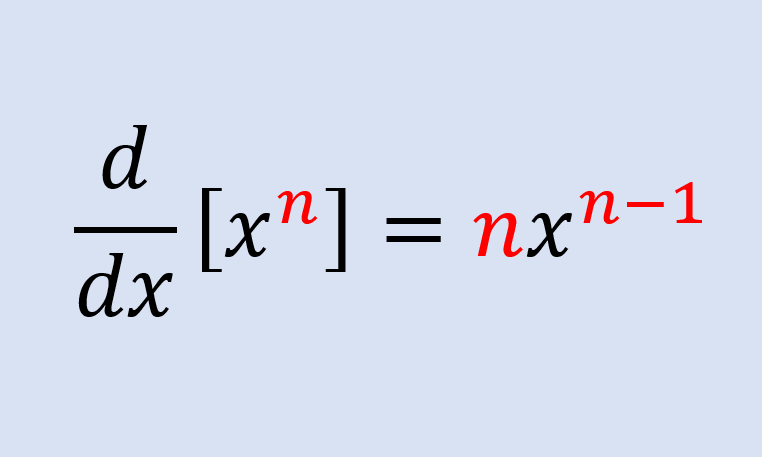
Relevante para…
Aprender a demostrar la regla de la potencia con diferentes métodos.
CÁLCULO
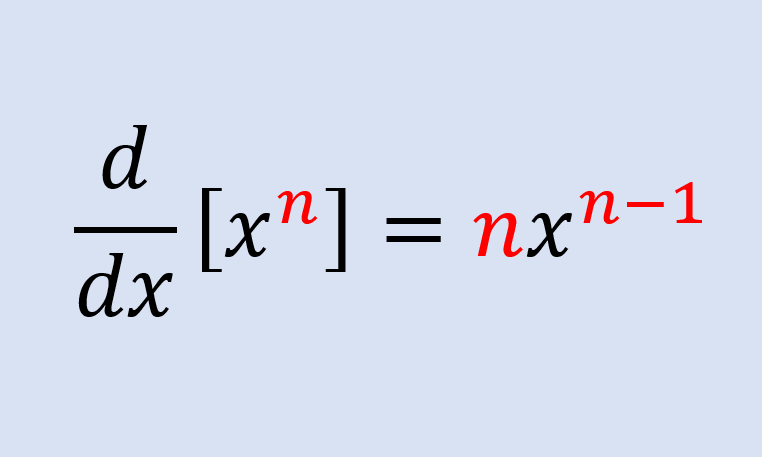
Relevante para…
Aprender a demostrar la regla de la potencia con diferentes métodos.
¿Qué es la regla de la potencia?
La regla de la potencia se define como la derivada de una variable elevada a un exponente numérico. Esta regla, sin embargo, solo se limita a variables con exponentes numéricos. Por lo tanto, las variables o funciones elevadas a otra variable o función no pueden usar esta regla.
La regla de la potencia se puede usar para derivar cualquier variable elevada a exponentes como los siguientes casos:
✔️ Elevada a un exponente positivo:
$latex y = x^n$
donde $latex x$ es una variable y $latex n$ es el exponente numérico positivo
✔️ Elevada a un exponente negativo (función racional en forma exponencial):
$latex y = \frac{1}{x^n}$
$latex y = x^{-n}$
donde $latex x$ es una variable y $latex n$ es el exponente numérico negativo
✔️ Elevada a un exponente racional (función radical en forma exponencial):
$latex y = \sqrt[n_2]{x^{n_1}}$
$latex y = x^{\frac{n_1}{n_2}}$
donde $latex x$ es una variable y $latex \frac{n_1}{n_2} = n$ o el exponente numérico racional $latex n$
Y la regla de la potencia no se puede usar para derivar:
❌ Elevada a un exponente variable:
$latex y = x^x$
❌ Elevada a cualquier tipo de función:
$latex y = x^{f(x)}$
Pero, ¿cómo derivamos exactamente estas funciones dadas usando la regla de la potencia?
La regla de la potencia se puede escribir de la siguiente manera:
| $latex f'(x^n) = nx^{n-1}$ |
en donde
- $latex x$ es la variable
- $latex n$ es el valor del exponente numérico de la variable $latex x$
En las funciones polinómicas, la regla de la potencia también se usa para cada término y se apoya en su totalidad en la suma/diferencia de derivadas.
En casos especiales de funciones trascendentales elevadas a un exponente numérico, la regla de la potencia se apoya en la fórmula de la regla de la cadena, usando la regla de la potencia como la derivada de la función exterior f de la función compuesta $latex f(g(x))$.
No debemos tomar esta fórmula a la ligera si pretendemos comprender en profundidad cómo se deriva una variable elevada a un exponente numérico. Para aprender y comprender los conceptos detrás del desarrollo de esta fórmula de la regla de la potencia, debemos estar familiarizados con cualquier demostración que satisfaga el enunciado de la regla de la potencia.
Demostración de la regla de la potencia usando el teorema del binomio
Para comprender mejor la demostración de la regla de la potencia mediante el teorema del binomio, se recomienda estar familiarizado con los temas El teorema del binomio, La pendiente de una recta tangente y Derivadas mediante límites.
Podemos recordar que
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} \left( {\frac{f(x+h)-f(x)}{h}} \right)$$
Al aplicar límites, podemos derivar una función f(x). Pero, ¿qué tal si $latex f(x) = x^n$? Si ese es el caso, tenemos
$$ \frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{(x+h)^n – x^n}{h}} \right)$$
Podemos evaluar $latex (x+h)^n$ aplicando el teorema del binomio. Antes de aplicarlo a nuestro límite, podemos recordar que el teorema del binomio es un método algebraico para desarrollar una expresión binomial.
El teorema del binomio ilustra que para expandir una cantidad de un binomio elevado a un exponente numérico, tenemos
$$(a+b)^n = \displaystyle \sum_{k=0}^{n} {n\choose k} a^{n-k} b^k$$
en donde
- $latex a$ y $latex b$ pueden ser una variable o una constante
- $latex n$ es el exponente del binomio
- $latex k$ es el orden de potencia del polinomio en la sumatoria.
- $latex {n \choose k}= \frac{n!}{k!(n-k)!}$; también llamada combinatoria $latex n$ escoge a $latex k$ o $latex {}_n C_k$
Expandiendo la sumatoria, tenemos
$$(a+b)^n = {n\choose 0} a^{n-0} b^0 + {n \choose 1} a^{n-1} b^{1}+ …… + {n \choose n-1} a^{n-(n-1)} b^{n-1} + {n\choose n} a^{n-n} b^{n}$$
$$(a+b)^n = \left(\frac{n!}{0! (n-0)!} \right) \cdot a^n + \left(\frac{n!}{1! (n-1)!} \right) \cdot a^{n-1} b+ …… + \left(\frac{n!}{(n-1)! (n-(n-1))!} \right) \cdot a^1 b^{n-1}+ \left(\frac{n!}{n! (n-n)!} \right) \cdot a^0 b^{n}$$
$$(a+b)^n = a^n + na^{n-1} b + …… + nab^{n-1} + b^{n}$$
Aplicando el teorema del binomio sobre $latex (x+h)^n$, tenemos
$$(x+h)^n = x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n$$
Sustituyendo esto en nuestra ecuación del límite, tenemos
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n – x^n}{h}} \right)$$
Simplificando un poco el numerador ya que hay términos similares que se pueden restar, tenemos
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{nx^{n-1} h + …… + nxh^{n-1} + h^n}{h}} \right)$$
Pero, ¿cómo podemos eliminar el denominador $latex h$ para evitar un resultado indefinido? Observa que todos los términos del numerador se multiplican por al menos $latex h$ y su mínimo común denominador es $latex h$. Por lo tanto, podemos dividir a cada término por $latex h$:
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( { \left(\frac{nx^{n-1} h}{h} \right)+ …… + \left( \frac{nxh^{n-1} + h^n}{h} \right) } \right)$$
$$ \frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1} h^{1-1}+ …… + nxh^{(n-1)-1} + h^{n-1} \right)$$
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1}+ …… + nxh^{n} + h^{n-1} \right)$$
Al evaluar nuestros límites a través del método de sustitución, tenemos
$$\frac{d}{dx} (x^n) = nx^{n-1}+ …… + nx(0)^{n} + (0)^{n-1} $$
Sabemos que cero elevado a cualquier exponente excepto 0 y $latex \infty$ es igual a cero, por lo que tenemos
| $latex f'(x^n) = nx^{n-1}$ |
que ahora es la fórmula de la regla de la potencia.
Demostración de la regla de la potencia mediante diferenciación logarítmica
Este es en realidad el método más corto para demostrar la fórmula de la regla de la potencia. Sin embargo, para comprender mejor esta demostración se recomienda estar familiarizado con el tema La diferenciación logarítmica, como requisito previo.
Podemos recordar que la diferenciación logarítmica consiste en convertir ambos lados de la ecuación en un logaritmo. Esto se usa, la mayoría de las veces, junto con la diferenciación implícita.
Por ejemplo, supongamos que tenemos la ecuación:
$latex y = x^n$
la cual al ser derivada es igual a
$latex y’ = f'(x^n)$
Pero, ¿cómo podemos derivar esto suponiendo que aún no conocemos la fórmula de la regla de potencia?
Evaluando $latex y = x^n$ logarítmicamente para eliminar el exponente $latex n$, tenemos
$latex \ln{(y)} = \ln{(x^n)}$
Aplicando propiedades logarítmicas, tenemos
$latex \ln{(y)} = n \ln{(x)}$
Para diferenciar, podemos usar diferenciación logarítmica en ambos lados de la ecuación:
$latex \frac{d}{dx} (\ln{(y)}) = \frac{d}{dx} (n \ln{(x)})$
Dado que el exponente $latex n$ solo debe limitarse a números reales, trataremos a $latex n$ como un coeficiente. Por lo tanto, tenemos
$latex \frac{d}{dx} (\ln{(y)}) = n \frac{d}{dx} (\ln{(x)})$
Entonces, aplicando diferenciación logarítmica, tenemos:
$latex \frac{y’}{y} = \frac{n}{x}$
Igualando la ecuación en términos de $latex y’$ o $latex f'(x^n)$, tenemos
$latex f'(x^n) = \frac{ny}{x}$
Sabemos que, $latex y = x^n$, por lo tanto, sustituimos $latex y$ en la ecuación derivada:
$latex f'(x^n) = \frac{n(x^n)}{x}$
Aplicando las leyes de los exponentes, tenemos
$latex f'(x^n) = nx^n \cdot x^{-1}$
| $latex f'(x^n) = nx^{n-1}$ |
que ahora es la fórmula de la regla de la potencia.
Veáse también
¿Interesado en aprender más sobre la regla de la potencia? Echa un vistazo a estas páginas:
- Regla de la potencia de derivadas – Fórmula y Ejemplos
- Ejercicios de la regla de la potencia de derivadas


