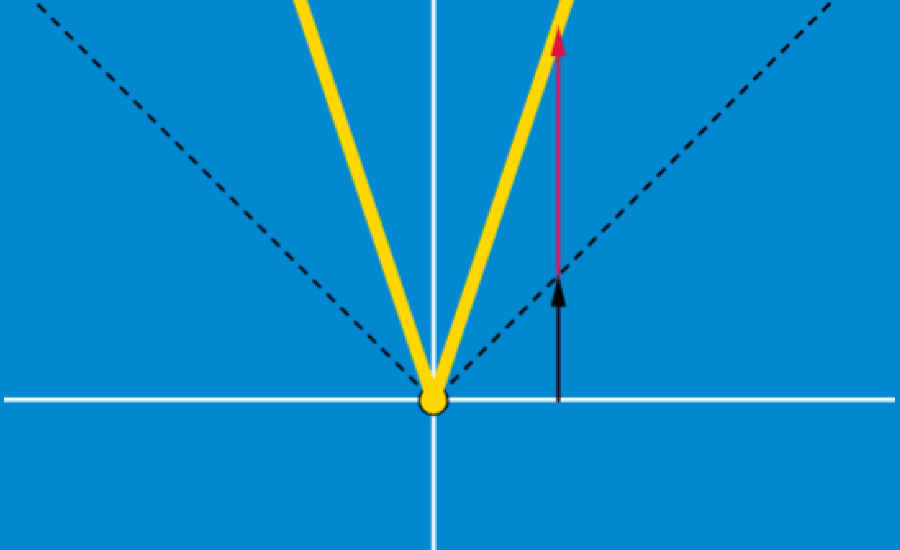
El valor absoluto de un número es la distancia desde 0 hasta ese número en la recta numérica. El valor absoluto se relaciona con la medida de distancias o diferencias en los casos en donde la dirección no es importante.
A continuación, miraremos una definición más detallada del valor absoluto, aprenderemos sobre sus propiedades y conoceremos algunas de sus aplicaciones en la vida real.
¿Qué es el valor absoluto?
El valor absoluto se refiere a la distancia de un punto desde el cero u origen en la recta numérica, sin importar la dirección. El valor absoluto siempre es positivo.
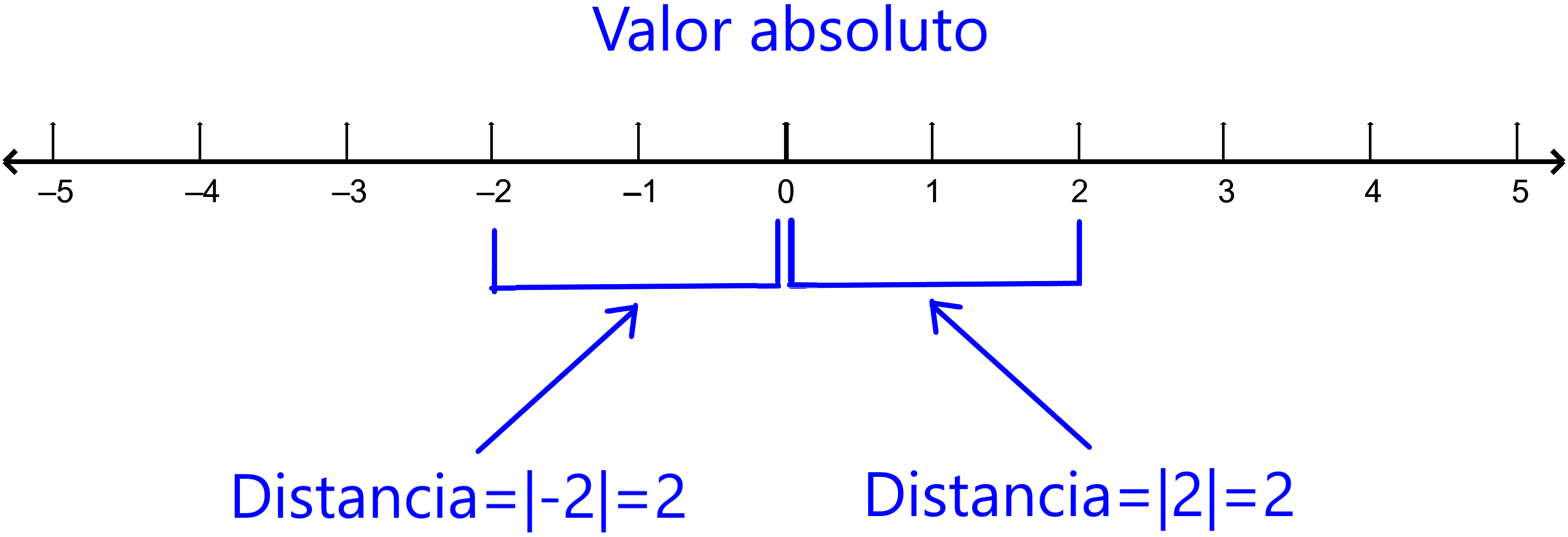
El valor absoluto es denotado por dos líneas verticales que encierran al número o a la expresión. Por ejemplo, el valor absoluto del número 3 es escrito |3|. Esto significa que la distancia desde 0 es 3.
De igual forma, el valor absoluto de 3 negativo es escrito |-3|. Esto también significa que la distancia desde 0 es 3.
Consideremos la expresión |x|>3. Para representar a esto en la recta numérica, necesitamos todos los números que tienen un valor absoluto mayor que 3. Esto puede ser graficado al colocar un punto abierto en la recta numérica.
Ahora consideremos la expresión |x|≤3. Esta expresión incluye todos los valores absolutos que son iguales o menores que 3. Podemos graficar esta expresión al colocar un punto cerrado en la recta numérica.
Una manera fácil de representar al valor absoluto con desigualdades es de la siguiente manera:
- Para |x|<3, podemos escribir -3<x<-3.
- Para |x|=5, podemos escribir x=5 o x=-5.
- Para |x+2|>3, podemos escribir 3>x+2>-3.
Propiedades del valor absoluto
El valor absoluto tiene las siguientes propiedades fundamentales:
1. No-negatividad |x| ≥ 0.
2. Multiplicatividad |xy| = |x| |y|.
3. Subaditividad |x+y| ≤ |x|+|y|.
4. Idempotencia ||x|| = |x|.
5. Simetría |-x| = |x|.
6. Identidad de discernible |x-y| = 0, ⇔ x=y.
Triangle of inequality |x-y| ≤ |x-z| + |z-y|.
8. Preservación de división |x/y| = |x|/|y|, si es que y≠0.
¿Cuáles son las aplicaciones del valor absoluto?
Existen varias aplicaciones del valor absoluto en matemáticas y en otras áreas. Algunas de las aplicaciones más comunes son:
1. Medir distancia
La medida de la distancia es una de las aplicaciones más comunes del valor absoluto. La distancia es el valor absoluto de la diferencia en posición entre dos puntos.
Entonces, dados dos puntos A y B, la distancia entre ellos es |A-B| que es equivalente a |B-A|. La distancia no depende de la dirección. En general, el valor absoluto es usado cuando la dirección no es importante.
2. Ecuaciones e inecuaciones con valor absoluto
El valor absoluto se utiliza para resolver ecuaciones y desigualdades que implican la distancia entre dos valores. Por ejemplo, la ecuación |x-3| = 5 tiene las soluciones x = -2 y x = 8.
3. Módulo de números complejos
El valor absoluto de un número complejo también se conoce como su módulo. Se utiliza para hallar la distancia del número complejo al origen en el plano complejo.
4. Análisis de datos
El valor absoluto se utiliza en estadística y análisis de datos para hallar la diferencia entre dos valores, como la diferencia entre la media y un punto de datos.
5. Física e ingeniería
El valor absoluto se utiliza en física e ingeniería para hallar la magnitud de magnitudes físicas como la velocidad, la aceleración y la fuerza.
6. Desviaciones de la norma
Una función valor absoluto puede ser usada para mostrar por cuánto se desvía un valor de la norma. Por ejemplo, la temperatura interna promedio de los humanos es 37° C. La temperatura puede variar por 0.5° C y seguir siendo considerada normal.
Como una función, podemos tener la ecuación y=|x-37|. Si es que graficáramos esta función, el eje x representaría a la temperatura actual y el eje y representaría la desviación de la temperatura de la temperatura promedio.
7. Retiros bancarios, tarjetas de crédito y la naturaleza del dinero
Aunque exista un saldo negativo en alguna cuenta de débito o de ahorro cuando se deba dinero al banco, nunca podrá retirar una cantidad negativa de dinero de las ventanillas del banco o de los cajeros automáticos.
El signo negativo en su saldo solo indica que tiene una obligación de devolver al banco que, una vez pagada, solo volverá a cero (si se paga exactamente) o a una cantidad positiva (si se paga o deposita más que el saldo negativo).
Lo mismo puede decirse de las tarjetas de crédito, en las que el banco te presta dinero por adelantado periódicamente. Esto significa que no importa lo negativo o positivo que sea tu saldo, no existe una cantidad negativa de dinero.
En general, el valor absoluto es un concepto versátil que puede aplicarse en muchos campos diferentes para representar la distancia entre dos valores, la magnitud de un número o una cantidad física, etc.
Véase también
¿Quieres saber más sobre las expresiones algebraicas? Consulta estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
