La cosecante de un ángulo es definida con respecto a los lados de un triángulo rectángulo. En un triángulo rectángulo, la cosecante es igual a la longitud de la hipotenusa dividida por el lado opuesto al ángulo. La cosecante es la función recíproca del seno.
A continuación, conoceremos más detalles sobre la cosecante y usaremos diagramas para facilitar el entendimiento. También, obtendremos los valores de la cosecante de los ángulos más importantes. Finalmente, veremos algunos ejercicios de práctica.
Definición de la cosecante de un ángulo
La cosecante de un ángulo es definida usando a un triángulo rectángulo. La cosecante de un ángulo es igual a la longitud de la hipotenusa dividida por la longitud del lado opuesto al ángulo en el triángulo.
Otra definición de las cosecantes es que son las funciones recíprocas del seno. Esto significa que la cosecante de un ángulo es igual a 1 dividido por el seno del ángulo. Sabemos que el seno es igual al lado opuesto dividido por la hipotenusa y la cosecante es lo inverso de eso. Entonces, tenemos:
$latex \csc (\theta)=\frac{1}{\sin}=\frac{H}{O}$
en donde, H es la hipotenusa y O es el lado opuesto.
Fórmula de la cosecante en triángulos rectángulos
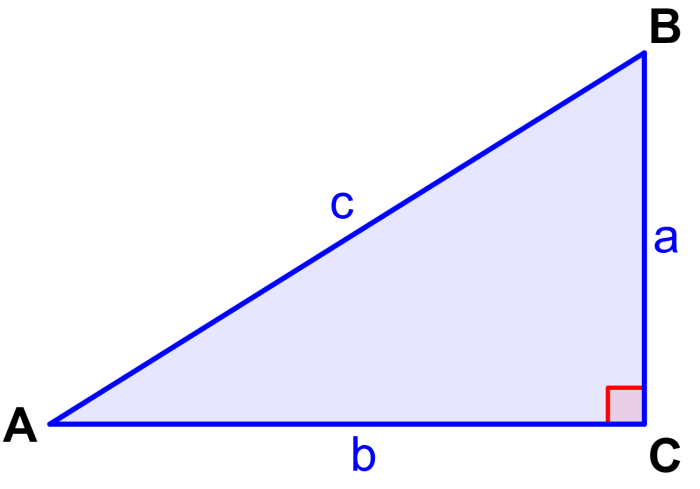
Podemos encontrar la fórmula de la cosecante de los ángulos en el siguiente triángulo rectángulo ABC.
Generalmente, usamos letras mayúsculas para representar a los ángulos y letras minúsculas para representar a los lados del triángulo opuestos al ángulo correspondiente. Por ejemplo, el lado a es opuesto al ángulo A, el lado b es opuesto al ángulo B y el lado c es opuesto al ángulo C.
Sabemos que la cosecante de un ángulo en un triángulo rectángulo es igual a la hipotenusa dividida por el lado opuesto:
| $latex \csc=\frac{\text{hipotenusa}}{\text{opuesto}}$ |
En el triángulo de arriba, tenemos $latex \csc(A)=\frac{c}{a}$ y también $latex \csc(B)=\frac{c}{b}$.
Cosecantes para ángulos especiales comunes
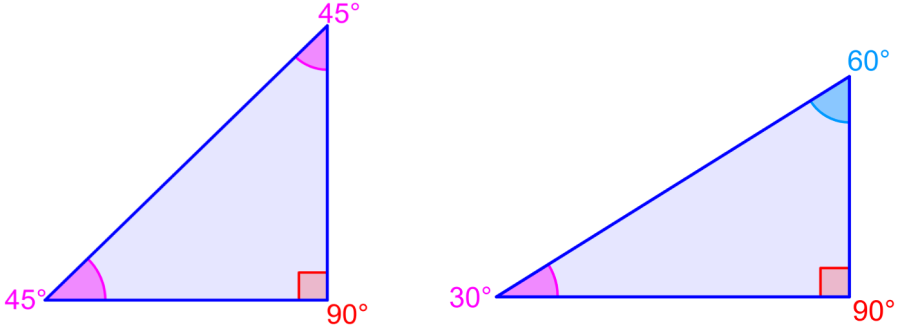
Los valores de las cosecantes para ángulos comunes pueden ser obtenidos usando las proporciones de los lados de triángulos especiales. Por ejemplo, podemos encontrar el valor de la cosecante de 45° usando al triángulo 45°-45°-90°.
Las proporciones de este triángulo son encontradas usando el teorema de Pitágoras: $latex {{c}^2}={{a}^2}+{{b}^2}$. Debido a que tenemos dos ángulos iguales de 45°, sabemos que $latex a=b$, por lo que el teorema de Pitágoras se vuelve $latex {{c}^2}=2{{a}^2}$. Esto significa que $latex c=a \sqrt{2}$.
Entonces, la cosecante de 45° es igual a $latex \sqrt{2}$.
Los valores de la cosecante de 30° y 60° son encontrados usando al triángulo 30°-60°-90°. Este triángulo tiene las proporciones 1:$latex \sqrt{3}$:2. Al usar esto, tenemos $latex \csc(30^{\circ})=2$ y $latex \csc(60^{\circ})=\frac{2}{\sqrt{3}}$, lo cual es equivalente a $latex \frac{2\sqrt{3}}{3}$.
Además, podemos encontrar los valores de las cosecantes de los ángulos 0° y 90° usando al círculo unitario. Cuando el ángulo es 0°, el lado opuesto es igual a 0 y no podemos dividir por 0, por lo que la cosecante es indefinida. Cuando el ángulo es 90°, el lado opuesto es igual a 1 y la hipotenusa es igual a 1, por lo que la cosecante es igual a 1.
| Grados | Radianes | Cosecante |
| 90° | $latex \frac{\pi}{2}$ | 1 |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{2\sqrt{3}}{3}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \sqrt{2}$ |
| 30° | $latex \frac{\pi}{6}$ | $latex 2$ |
| 0° | 0 | Indefinido |
Ejercicios de cosecante de un ángulo resueltos
La relación entre la cosecante y los lados de un triángulo rectángulo es usada para resolver los siguientes ejercicios. Cada uno de los siguientes ejercicios hace referencia al triángulo rectángulo visto arriba, por lo que la notación de los lados es la misma.
EJERCICIO 1
Si es que tenemos $latex \csc(A)=1.4$ y $latex a=6$, ¿cuál es el valor de c?
Solución
Haciendo referencia al triángulo rectángulo de arriba, tenemos $latex \csc(A)=\frac{c}{a}$. Usamos esta relación junto con los valores dados para encontrar el valor de c:
$latex \csc(A)=\frac{c}{a}$
$latex 1.4=\frac{c}{6}$
$latex c=1.4(6)$
$latex c=8.4$
El valor del lado c es igual a 8.4.
EJERCICIO 2
Determina el valor de b si es que tenemos $latex c=12$ y $latex \csc(B)=2.9$.
Solución
Tenemos los valores $latex c=12$ y $latex \csc (B)=2.9$. Usando estos valores en la relación $latex \csc(B)=\frac{c}{b}$, tenemos:
$latex \csc(B)=\frac{c}{b}$
$latex 2.9=\frac{12}{b}$
$latex b=\frac{12}{2.9}$
$latex b=4.14$
El valor de b es 4.14.
EJERCICIO 3
Tenemos los valores $latex c=4$ y $latex a=2\sqrt{3}$. ¿Cuál es el valor del ángulo A?
Solución
Usamos al triángulo rectángulo de arriba como referencia para formar la relación $latex \csc(A)=\frac{c}{a}$. Entonces, usando los valores dados, tenemos:
$latex \csc(A)=\frac{c}{a}$
$latex \csc(A)=\frac{4}{2\sqrt{3}}$
$latex \csc(A)=\frac{2\sqrt{3}}{3}$
Podemos usar una calculadora con $latex {{\csc}^{-1}}$ o la tabla de arriba para determinar que:
$latex A=60$°
El águlo A mide 60°.
→ Calculadora de Cosecante (Grados y Radianes)
Ejercicios de cosecante de un ángulo para resolver
Resuelve los siguientes ejercicios de práctica usando lo aprendido sobre la cosecante de un ángulo. Estos ejercicios hacen referencia al triángulo rectángulo visto arriba, por lo que usan la misma notación para los lados y los ángulos.
Véase también
¿Interesado en aprender más sobre cosecantes, secantes y cotangentes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
