Para saber si una función tiene inversa, podemos usar la prueba de la línea horizontal con su gráfica. Si cualquier línea horizontal trazada cruza a la función más de una vez, entonces, la función no tiene inversa. Para que una función tenga inversa, cada salida de la función debe ser producida por una sola salida.
Mira los siguientes ejemplos para comprender esta idea completamente.
Definición de función inversa
Antes de empezar con las inversas de funciones, tenemos que revisar brevemente a las funciones.
Consideremos a la función $latex f(x)=2x-3$. Sabemos cómo evaluar la función f en 2, $latex f(2)=2(2)-3=1$. Podemos pensar en la función f como algo que transforma el 2 en el 1 y el 4 en el 5:
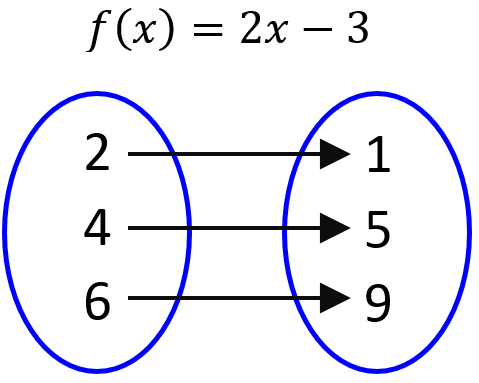
Entonces, dado que la función f está actuando en los números y transformándolos, podemos pensar en la inversa de f como algo que “revierte” el efecto de la función f. Es decir, la inversa de f debe tomar el 1 como entrada y producir el 2 y tomar el 5 para producir el 4.
Supongamos que tenemos la función $latex g(x)=\frac{x+3}{2}$. Al evaluarla con la entrada 1, resulta en $latex g(1)=\frac{1+3}{2}=2$ y al evaluarla con la entrada 5, resulta en $latex g(5)=\frac{5+3}{2}=4$. Podemos ver que la función g pareciera revertir el efecto de la función f.
Para probar que la función g es la inversa de f, debemos mostrar que esto es verdadero para cualquier valor de x en el dominio de f. Es decir, la función g debe tomar a f(x) y retornar x.
Entonces, $latex g(f(x))=x$ debe ser verdadero para todos los valores de x en el dominio de f. Una forma de verificar esto es simplemente, comprobando si es que $latex g(f(x))$ retorna x:
$latex g(f(x))=\frac{2x-3+3}{2}$
$latex g(f(x))=\frac{2x}{2}$
$latex g(f(x))=x$
Usando $latex {{f}^-1}$ para denotar a la inversa de f, acabamos de mostrar que $latex g={{f}^{{-1}}}$.
Gráficas de funciones inversas
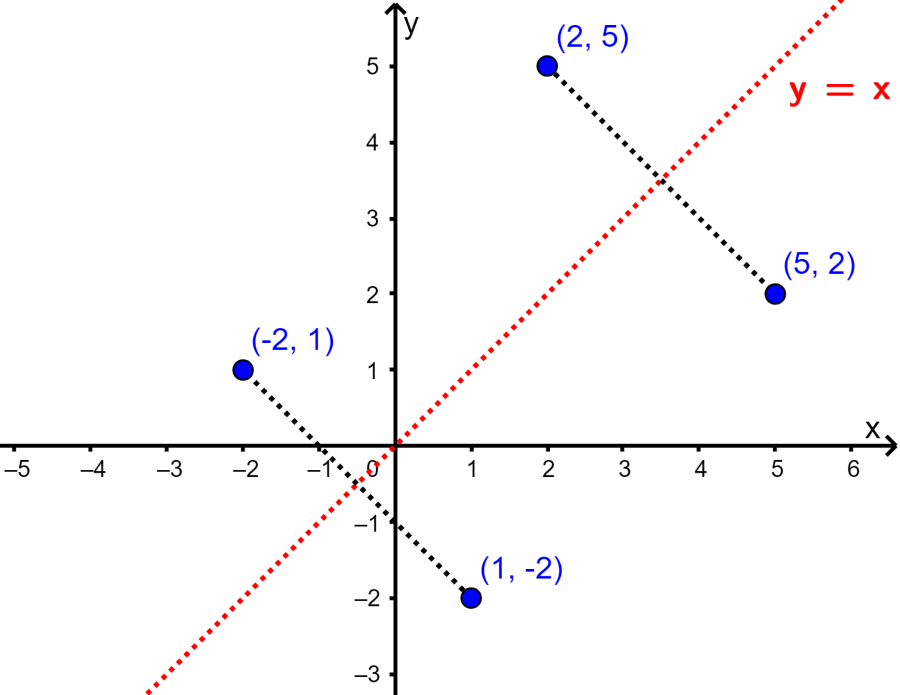
Sabemos que la reflexión de un punto (a, b) con respecto al eje x es (a, -b) y la reflexión de (a, b) con respecto al eje y es (-a, b). Ahora queremos reflejar con respecto a la línea $latex y=x$. La siguiente gráfica ilustra la reflexión del punto (a, b) con respecto a la línea $latex y=x$ para formar el punto (b, a):
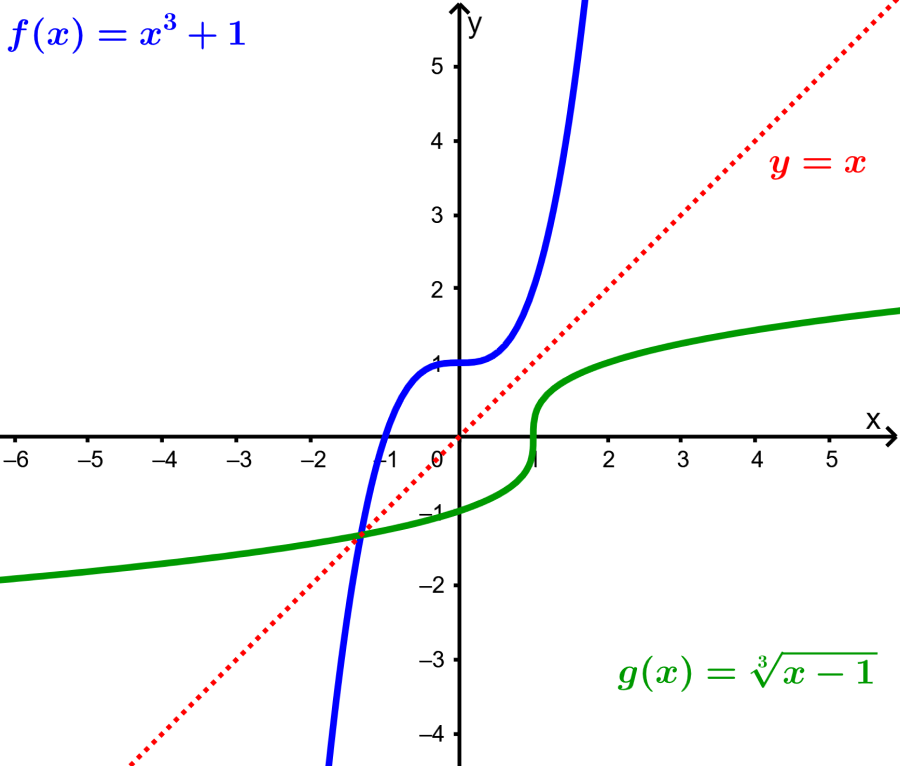
Si es que tenemos la función $latex f(x)={{x}^3}+1$, entonces tenemos $latex f(1)=2$ y el punto (1, 2) está en la gráfica de f. La función inversa de f debe tomar como entrada al 2 y producir el 1 como salida, es decir, $latex {{f}^{{-1}}}(2)=1$ y el punto (2, 1) está en la gráfica de $latex {{f}^{{-1}}}$.
El punto (2, 1) es la reflexión del punto (1, 2) con respecto a la línea $latex y=x$. Lo mismo sucede con el resto de puntos en la gráfica de f, por lo que la inversa es la gráfica que resulta al reflejar a la gráfica de f con respecto a la línea $latex y=x$:
¿Cómo saber si una función tiene inversa?
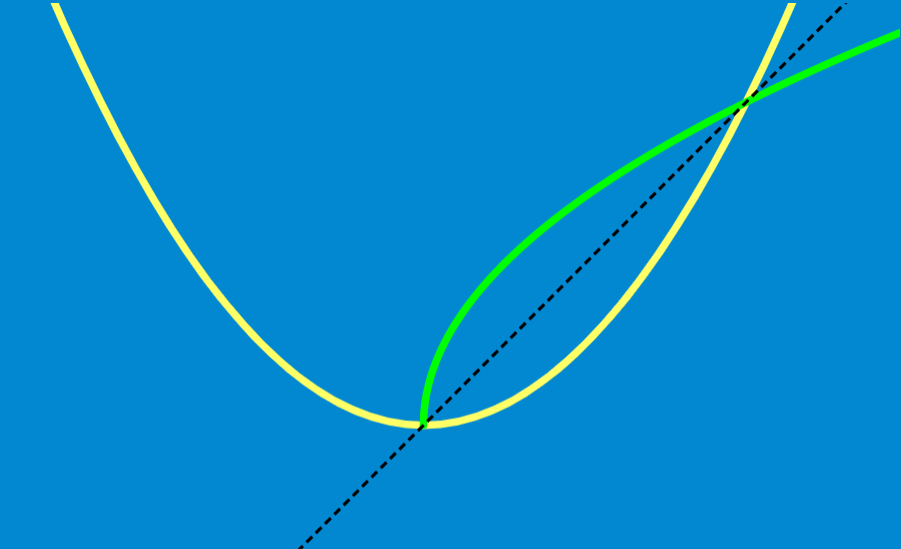
Algunas funciones no tienen inversas. Por ejemplo, supongamos que tenemos la función $latex f(x)={{x}^2}$. La función puede tomar dos números diferentes y producir la misma salida, por ejemplo, $latex f(3)=9$ y $latex f(-3)=9$. Si es que f tuviera una inversa, esto significaría que esta función debería tomar 9 para producir tanto 3 como -3.
Sin embargo, esto va contrario a la definición de una función, la cual indica que cada entrada debe producir una única salida. Por lo tanto, no existe una función que es la inversa de f.
En términos de gráficas, si es que f tuviera una inversa, entonces, su gráfica sería una reflexión de la gráfica de f con respecto a $latex y=x$:
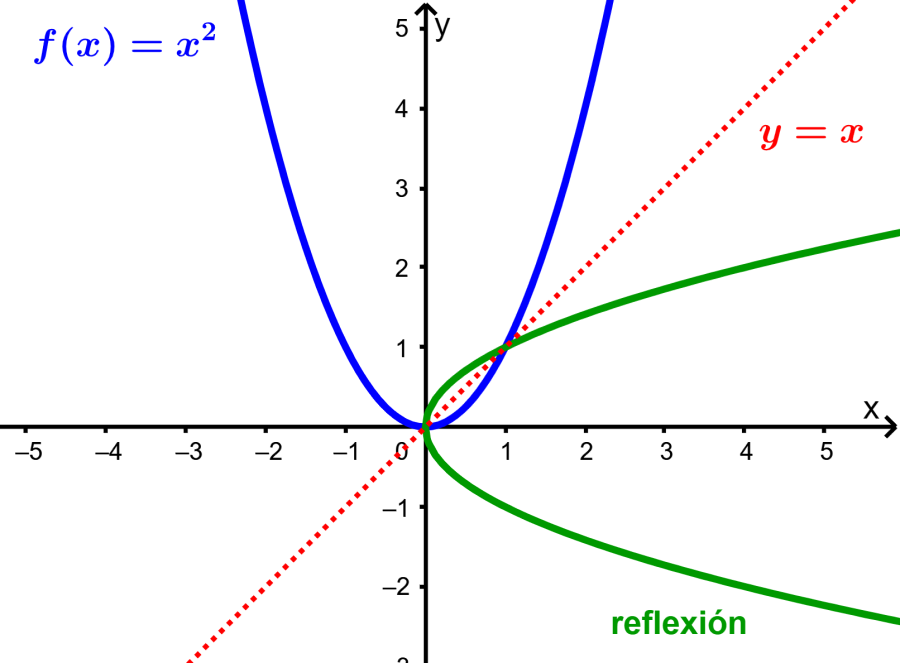
Podemos ver que la gráfica reflejada no pasa la prueba de la línea vertical, por lo que esa gráfica no representa a una función. Podemos generalizar esto de la siguiente manera:
Una función f tiene una inversa solo si es que cuando su gráfica es reflejada con respecto a $latex y=x$, el resultado es una gráfica que sí pasa la prueba de la línea vertical. Pero podemos simplificar esto. Podemos determinar antes de reflejar la gráfica si es que la función tiene una inversa o no al usar la prueba de la línea horizontal.
Prueba de la línea horizontal
Tenemos la función f. La prueba de la línea horizontal nos indica que:
- Si es que cualquier línea horizontal interseca a la gráfica de f más de una vez, entonces, f no tiene una inversa.
- Si es que cualquier línea horizontal no interseca a la gráfica de f más de una vez, entonces, f sí tiene una inversa.
EJEMPLOS
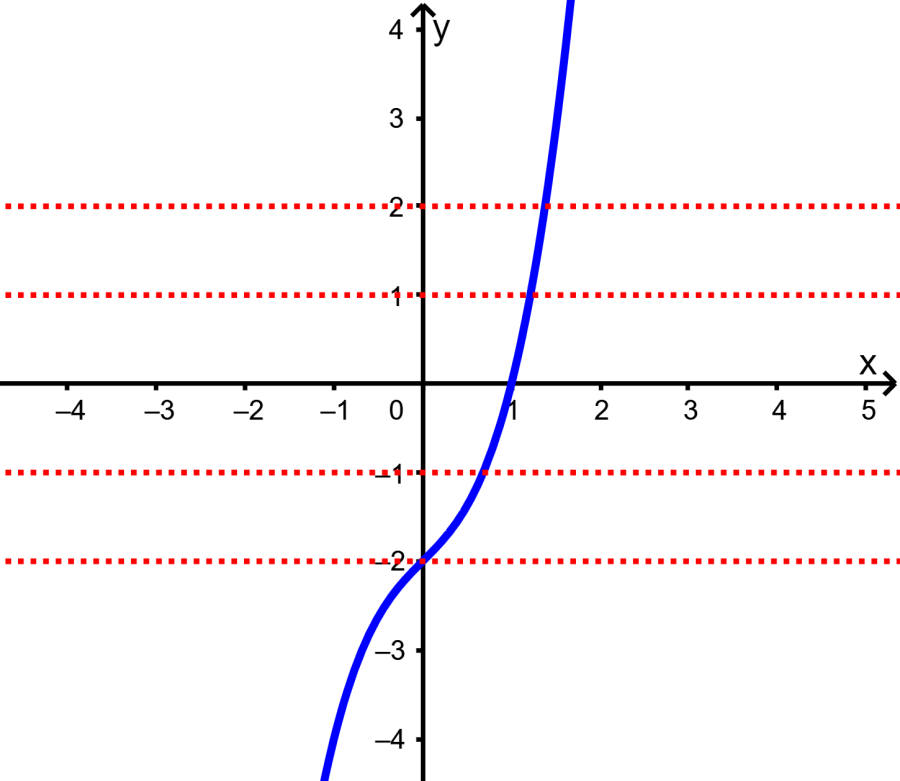
- Usando la prueba de la línea horizontal con la función $latex f(x)={{x}^3}+x-2$, podemos ver que la función sí pasa esta prueba, por lo que sí tiene una inversa.
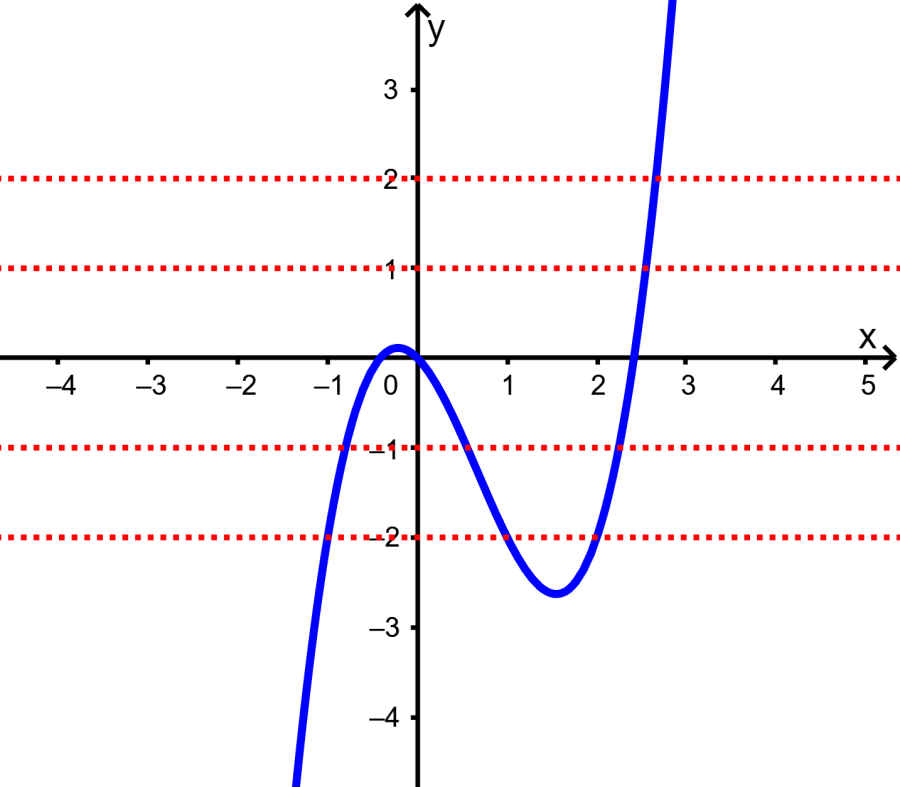
- Usando la prueba de la línea horizontal con la función $latex f(x)={{x}^3}-2{{x}^2}-x$, podemos ver que la función no pasa esta prueba, por lo que no tiene una inversa.
Encontrar funciones inversas
Empecemos considerando a una función simple $latex f(x)=2x+3$.
La gráfica de f es una línea con pendiente 2, por lo que pasa la prueba de la línea horizontal y tiene una inversa.
Hay dos pasos requeridos para evaluar f en un número x. Primero multiplicamos a la x por 2 y luego sumamos 3.
Para obtener la inversa de la función, debemos revertir esos efectos en orden contrario. Entonces, para formar la función inversa $latex {{f}^{{-1}}}$, empezamos revirtiendo la suma de 3 al restar 3. Luego, revertimos la multiplicación por 2 al dividir por 2. Entonces tenemos:
$latex {{f}^{{-1}}}(x)=\frac{x-3}{2}$
Pasos para encontrar la inversa de una función f
Paso 1: Reemplazamos f(x) por y en la ecuación de la función.
Paso 2: Intercambiamos las x y las y.
Paso 3: Resolvemos para y.
Paso 4: Reemplazamos y por $latex {{f}^{{-1}}}(x)$.
EJEMPLO 1
Encuentra la inversa de $latex f(x)=5-\frac{x}{3}$.
Paso 1: $latex y=5-\frac{x}{3}$
Paso 2: $latex x=5-\frac{y}{3}$
Paso 3: $latex y=15-3x$
Paso 4: $latex {{f}^{{-1}}}(x)=15-3x$
EJEMPLO 2
Encuentra la inversa de $latex f(x)={{x}^3}+5$.
Paso 1: $latex y={{x}^3}+5$
Paso 2: $latex x={{y}^3}+5$
Paso 3: $latex y=\sqrt[3]{{x-5}}$
Paso 4: $latex {{f}^{{-1}}}=\sqrt[3]{{x-5}}$
→ Calculadora de Función Inversa
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas: