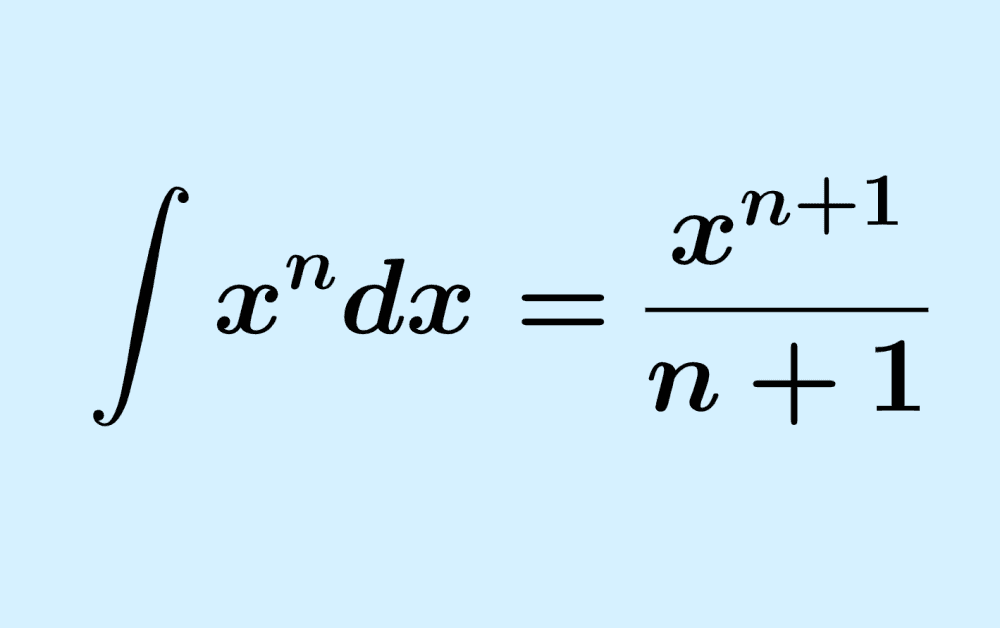La integral de un polinomio puede ser encontrada al sumar 1 a los exponentes de la variable de cada término del polinomio. Luego, multiplicamos a cada término por el recíproco del nuevo exponente. Finalmente, simplificamos la expresión obtenida y sumamos la constante de integración.
A continuación, resolveremos 10 ejercicios de integrales de polinomios. Luego, puedes poner a prueba tus habilidades con 5 ejercicios prácticos.
Proceso usado para encontrar la integral de una función polinómica
Para encontrar la integral de una función polinómica, usamos un proceso inverso al usado para diferenciar a un polinomio.
Por ejemplo, supongamos que queremos encontrar la integral de $latex \int x^4 dx$. Para esto, observamos que la derivada de $latex x^5$ es igual a $latex 5x^4$ y tendríamos la misma potencia de x.
Sin embargo, en este caso no necesitamos la constante 5, por lo que multiplicamos a $latex x^5$ por $latex \frac{1}{5}$. Entonces, tenemos
La derivada de $latex \frac{1}{5} x^5$ es $latex x^4$
Por lo tanto,
$$\int x^4 dx =\frac{1}{5}x^5+c$$
En general, tenemos la siguiente fórmula:
$$\int ax^n dx =\frac{ax^{n+1}}{n+1}+c$$
en donde, $latex n \neq -1$.
Podemos usar los siguientes pasos para encontrar la integral de cualquier polinomio:
Paso 1: Sumar 1 a los exponentes de cada término del polinomio.
Nota: Los términos constantes son equivalentes a tener la variable $latex x^0$, por lo que al sumar 1, tenemos $latex x^1=x$.
Paso 2: Multiplicar a cada término por el recíproco del nuevo exponente.
Nota: El recíproco de un número es igual a 1 sobre un número. Por ejemplo, el recíproco de 5 es $latex \frac{1}{5}$.
Paso 3: Simplifica la integral resultante y sumar el término constante $latex c$.
10 Ejercicios resueltos de integrales de polinomios
EJERCICIO 1
Encuentra la integral del polinomio $latex 3x^2+1$
Solución
Para resolver este ejercicio, tenemos que empezar formando la integral con el polinomio dado:
$latex \int 3x^2+1 dx$
Ahora, podemos obtener la integral al considerar lo siguiente:
- El exponente de cada variable a ser integrada tiene que ser sumado 1.
- Cada término del polinomio debe ser dividido por el nuevo exponente.
Aplicando esto, tenemos:
$$\int 3x^2+1 dx=\frac{3x^3}{3}+1x$$
Simplificando y añadiendo la constante de integración, tenemos:
$$\int 3x^2+1 dx=x^3+x+c$$
EJERCICIO 2
¿Cuál es la integral del polinomio $latex x^3+2x$?
Solución
Empezamos formando la integral con el polinomio dado:
$latex \int x^3+2x dx$
Ahora, podemos resolver la integral del polinomio al seguir los siguientes pasos.
- Sumamos 1 al exponente de cada término.
- Cada término debe ser dividido por el nuevo exponente.
Entonces, tenemos:
$$\int x^3+2x dx=\frac{x^4}{4}+\frac{2x^2}{2}$$
Cuando simplificamos y sumamos la constante de integración, tenemos:
$$\int x^3+2x dx=\frac{x^4}{4}+x^2+c$$
EJERCICIO 3
Determina la integral de la función polinomial $latex f(x)=-x^3-3x^2$.
Solución
Formando la integral con la función polinomial dada, tenemos:
$latex \int -x^3-3x^2 dx$
Ahora, aplicamos lo siguiente:
- Cada exponente de la variable a integrarse debe ser sumado por 1.
- Cada término debe ser dividido por el valor del nuevo exponente.
Entonces, tenemos:
$$\int -x^3-3x^2 dx=-\frac{x^4}{4}-\frac{3x^3}{3}$$
Cuando simplificamos y añadimos la contante de integración, tenemos:
$$\int -x^3-3x^2 dx=-\frac{x^4}{4}-x^3+c$$
EJERCICIO 4
¿Cuál es la integral de la función polinomial $latex f(x)=5x^3-3x-2$?
Solución
La integral a ser evaluada es:
$latex \int 5x^3-3x -2 dx$
Resolvemos la integral aplicando los siguientes pasos:
- Sumamos 1 al exponente de cada término del polinomio.
- Dividimos a cada término por el nuevo exponente.
Aplicando esto, tenemos:
$$\int 5x^3-3x -2 dx=\frac{5x^4}{4}-\frac{3x^2}{2}-2x$$
Simplificando y añadiendo la constante de integración, tenemos:
$$\int 5x^3-3x -2 dx=\frac{5x^4}{4}-\frac{3x^2}{2}-2x+c$$
EJERCICIO 5
Encuentra la integral del polinomio $latex 2x^3-6x^2+5x$.
Solución
Formando la integral a ser evaluada, tenemos:
$latex \int 2x^3-6x^2+5x dx$
Ahora, podemos aplicar lo siguiente para resolver la integral:
- El exponente de x de cada término debe ser sumado 1.
- Cada término debe ser dividido por el valor del nuevo exponente.
Cuando aplicamos esto, tenemos:
$$\int 2x^3-6x^2+5x dx=\frac{2x^4}{4}-\frac{6x^3}{3}+\frac{5x^2}{2}$$
Cuando simplificamos y sumamos la constante de integración, tenemos:
$$\int 2x^3-6x^2+5x dx=\frac{x^4}{2}-2x^3+\frac{5x^2}{2}+c$$
EJERCICIO 6
Si es que tenemos la función $latex f(x)=2x^4+3x^3-2x^2$, ¿cuál es su integral?
Solución
La integral a ser evaluada es:
$latex \int 2x^4+3x^3-2x^2 dx$
Cuando evaluamos esta integral, tenemos:
$$\int 2x^4+3x^3-2x^2 dx=\frac{2x^5}{5}+\frac{3x^4}{4}-\frac{2x^3}{3}$$
Simplificando y añadiendo la constante de integración, tenemos:
$$\int 2x^4+3x^3-2x^2 dx=\frac{2x^5}{5}+\frac{3x^4}{4}-\frac{2x^3}{3}+c$$
EJERCICIO 7
Encuentra la integral de la función $latex f(x)=3x^3+(x-2)^2$.
Solución
Podemos empezar expandiendo el binomio y simplificando la función polinomial dada:
$latex f(x)=3x^3+(x-2)^2$
$latex f(x)=3x^3+x^2-4x+4$
Formando la integral, tenemos:
$latex \int 3x^3+x^2-4x+4 dx$
Resolviendo la integral, tenemos:
$$\int 3x^3+x^2-4x+4 dx=\frac{3x^4}{4}+\frac{x^3}{3}-\frac{4x^2}{2}+4x$$
Cuando simplificamos y sumamos la constante de integración, tenemos:
$$\int 3x^3+x^2-4x+4 dx=\frac{3x^4}{4}+\frac{x^3}{3}-2x^2+4x+c$$
EJERCICIO 8
Encuentra la integral de $latex f(x)=2x^3+(x+4)^2-2x^2$.
Solución
Expandiendo el polinomio dado y simplificando, tenemos:
$latex f(x)=2x^3+(x+4)^2-2x^2$
$latex f(x)=2x^3+x^2+8x+16-2x^2$
$latex f(x)=2x^3-x^2+8x+16$
La integral a ser evaluada es:
$latex \int 2x^3-x^2+8x+16 dx$
Entonces, tenemos:
$$\int 2x^3-x^2+8x+16 dx=\frac{2x^4}{4}-\frac{x^3}{3}+\frac{8x^2}{2}+16x$$
Simplificando y añadiendo la constante de integración, tenemos:
$$\int 2x^3-x^2+8x+16 dx=\frac{x^4}{2}-\frac{x^3}{3}+4x^2+16x+c$$
EJERCICIO 9
Si es que la derivada de una curva es $latex g(x)=4x^3-2$ y la curva pasa a través del punto $latex (-1, ~2)$. Encuentra la ecuación de la curva.
Solución
En este problema, tenemos que encontrar la función de la curva que tiene una derivada igual a $latex g(x)=4x^3-2$. Es decir, tenemos que encontrar la integral de la derivada dada.
Entonces, formando la integral a ser evaluada, tenemos:
$latex \int 4x^3-2 dx$
Resolviendo esto, tenemos:
$$\int 4x^3-2 dx=\frac{1}{4}4x^4-2x+c$$
$$\int 4x^3-2 dx=x^4-2x+c$$
Podemos determinar el valor de la constante de integración al usar el punto $latex (-1, ~2)$. Entonces, tenemos:
$latex y=x^4-2x+c$
$latex 2=(-1)^4-2(-1)+c$
$latex 2=1+2+c$
$latex c=-1$
Entonces, la ecuación de la curva es $latex y=x^4-2x-1$.
EJERCICIO 10
Una curva tiene una pendiente representada por $latex 20x^4-10x$. Si es que la curva pasa por el punto (1, 3), ¿cuál es su ecuación?
Solución
En este caso, conocemos la ecuación de la pendiente de la curva. Sin embargo, recordamos que la pendiente es igual a la derivada de la función.
Entonces, similar al ejercicio anterior, vamos a encontrar la integral de $latex 20x^4-10x$, ya que la integral representa la ecuación de la curva:
$latex \int 20x^4-10x dx$
Resolviendo esta integral, tenemos:
$$\int 20x^4-10x dx=\frac{20x^5}{5}-\frac{10x^2}{2}+c$$
$$\int 20x^4-10x dx=4x^5-5x^2+c$$
Si es que usamos el punto (1, 3), podemos determinar el valor de la constante:
$latex y=4x^5-5x^2+c$
$latex 3=4(1)^5-5(1)^2+c$
$latex 3=4-5+c$
$latex c=4$
Entonces, la ecuación de la curva es $latex y=4x^5-5x^2+4$.
Ejercicios de integrales de polinomios para resolver
Si es que tenemos $latex F(x)=\int f(x)dx$, encuentra el valor de $latex F(2)$ si es que $latex c=0$ para la función: $$f(x)=4x^3+6x^2-5x-10$$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
