La circunferencia de un círculo define a la longitud del contorno del círculo. La circunferencia también es denominada como el perímetro del círculo, ya que es una medida de los límites del círculo. La circunferencia puede ser calculada usando la longitud del diámetro o la longitud del radio y la constante π.
A continuación, aprenderemos sobre la circunferencia del círculo más a detalle. Descubriremos cuál es su fórmula y aprenderemos su origen. Además, conoceremos sobre el origen de la contante π. Finalmente, resolveremos algunos ejercicios en donde aplicaremos la fórmula de la circunferencia.
Fórmula de la circunferencia de un círculo
La circunferencia representa a la longitud obtenida al dar una vuelta completa alrededor del círculo. Esta longitud puede ser obtenida al usar la longitud del diámetro o el radio del círculo y la constante pi.
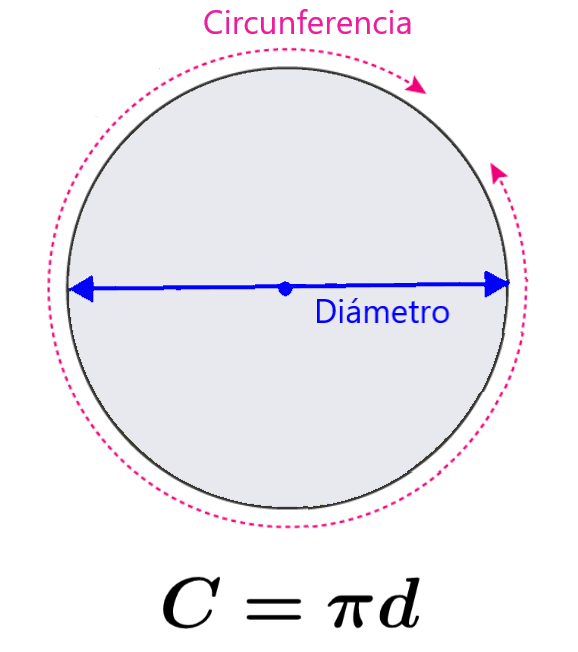
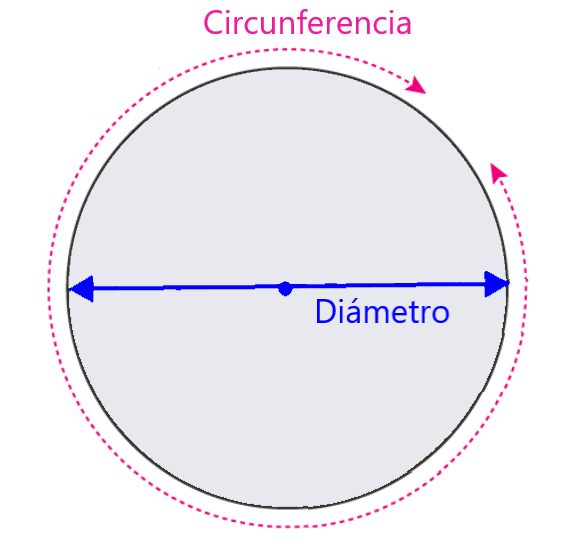
Recordemos que usamos la letra griega π para representar a esta constante y que tiene un valor aproximado de 3.141592… Para obtener una fórmula para la circunferencia, podemos considerar al siguiente círculo:
En el diagrama, podemos observar que la circunferencia es la distancia alrededor del círculo. Además, podemos ver que el diámetro es la distancia que pasa por el centro del círculo y conecta dos partes opuestas de la circunferencia.
La constante π representa a la proporción de la circunferencia del círculo al diámetro. Esto significa que cuando dividimos la circunferencia de cualquier círculo por el diámetro, obtenemos la constante π. Podemos expresar a esta relación con la siguiente fórmula:
$latex \frac{C}{d}=\pi$
en donde, C representa a la circunferencia y d es la longitud del diámetro del círculo. Además, podemos reescribir a esta expresión de la siguiente manera:
| $latex C=\pi d$ |
Circunferencia de un círculo con radio
La circunferencia de un círculo también puede ser calculada usando la longitud del radio. Para esto, usamos la relación $latex d=2r$. Al reescribir a la expresión, tenemos:
| $latex C=2\pi r$ |
Ejercicios de circunferencia de círculos resueltos
Los siguientes ejercicios son resueltos usando las fórmulas de la circunferencia de círculos. Es recomendable que resuelvas los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es la circunferencia de un círculo que tiene un diámetro de 5 m?
Solución
Tenemos la longitud del diámetro $latex d=5$. Entonces, usamos la primera fórmula:
$latex C=\pi d$
$latex C=\pi (5)$
$latex C=15.7$
La circunferencia es igual a 15.7 m.
EJERCICIO 2
Si es que un círculo tiene un diámetro de 9 m. ¿Cuál es la longitud de su circunferencia?
Solución
Podemos usar la primera fórmula de la circunferencia con el valor $latex d=9$:
$latex C=\pi d$
$latex C=\pi (9)$
$latex C=28.3$
La circunferencia es igual a 28.3 m.
EJERCICIO 3
¿Cuál es la longitud de la circunferencia de un círculo que tiene un radio de 4 m?
Solución
Aquí, tenemos la longitud del radio en vez del diámetro. Podemos usar la segunda fórmula con el valor $latex r=4$:
$latex C=2\pi r$
$latex C=2\pi (4)$
$latex C=50.3$
La longitud de la circunferencia es 50.3 m.
EJERCICIO 4
Un círculo tiene un radio de 11 m. ¿Cuál es su circunferencia?
Solución
Usamos la segunda fórmula de la circunferencia con el valor $latex r=11$. Entonces, tenemos:
$latex C=2\pi r$
$latex C=2\pi (11)$
$latex C=69.1$
La circunferencia es igual a 69.1 m.
EJERCICIO 5
Si es que un círculo tiene una circunferencia de 80 m, ¿cuál es la longitud de su diámetro?
Solución
Aquí, empezamos con el valor de la circunferencia y queremos encontrar la longitud del diámetro, por lo que usamos el valor $latex C=80$ en la fórmula y resolvemos para d:
$latex C=\pi d$
$latex 80=\pi d$
$latex d=\frac{80}{\pi}$
$latex d=25.5$
La longitud del diámetro es igual a 25.5 m.
Ejercicios de circunferencia de círculos para resolver
Usa las fórmulas de circunferencia de círculos para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre círculos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
