El volumen de un prisma hexagonal es calculado al multiplicar al área de la base hexagonal por la altura del prisma. Por otro lado, el área superficial del prisma hexagonal es calculada sumando las áreas de todas sus caras.
A continuación, conoceremos las fórmulas que podemos usar para calcular el área superficial y el volumen de prismas hexagonales. Además, usaremos estas fórmulas para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a calcular el volumen y el área de un prisma hexagonal.
GEOMETRÍA

Relevante para…
Aprender a calcular el volumen y el área de un prisma hexagonal.
¿Cómo calcular el volumen de un prisma hexagonal?
El volumen de un prisma hexagonal es calculado al multiplicar el área de la base por la altura del prisma. Estos poliedros tienen bases hexagonales, por lo que tenemos que calcular el área de un hexágono para encontrar el volumen. Recordemos que la siguiente es la fórmula del área de un hexágono:
$latex A=\frac{3sqrt{3}}{2}{{a}^2}$
en donde, a es la longitud de uno de los lados del hexágono.
Esta fórmula puede ser derivada al dividir al hexágono en seis triángulos congruentes y encontrar el área de uno de los triángulos.
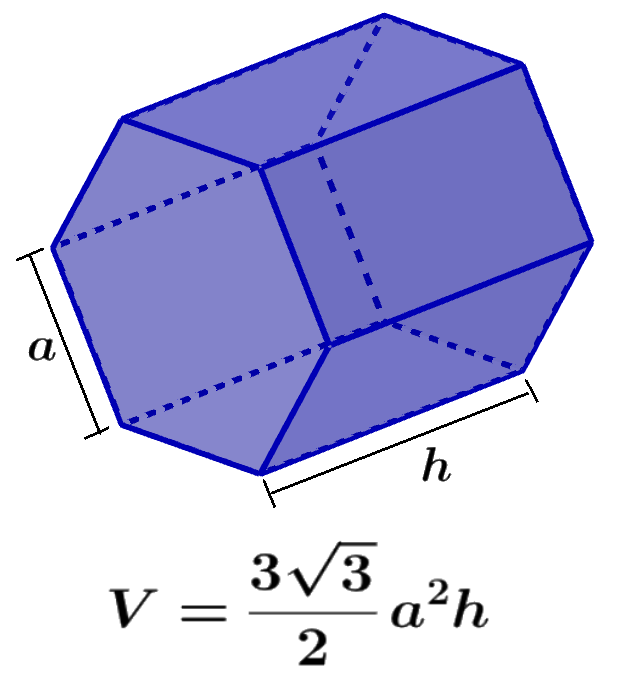
Dado que tenemos una fórmula para el área de la base del prisma hexagonal, la fórmula para su volumen es:
| $latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$ |
en donde, a es la longitud de uno de los lados de la base hexagonal y h es la longitud de la altura del prisma.
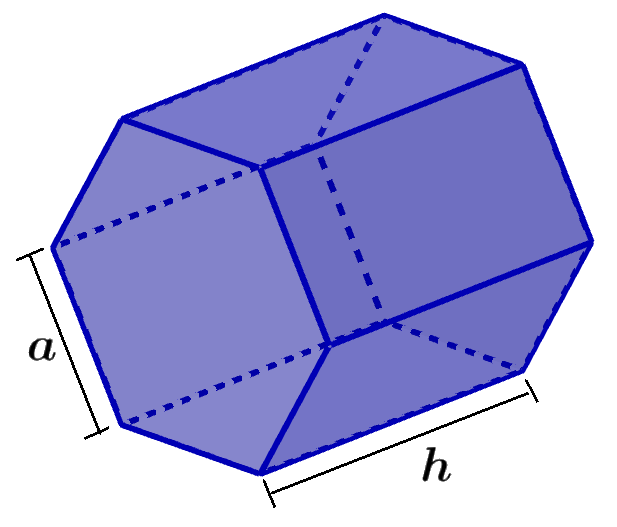
¿Cómo calcular el área superficial de un prisma hexagonal?
Para encontrar el área superficial de un prisma hexagonal, tenemos que sumar las áreas de todas sus caras.
Los prismas hexagonales tienen dos caras hexagonales que son paralelas y congruentes. Estos prismas también tienen seis caras rectangulares laterales que también son congruentes.
Entonces, empezamos encontrando expresiones para una cara hexagonal y una cara rectangular.
El área de un hexágono regular puede ser encontrada usando la fórmula: $latex A=\frac{3\sqrt{3}}{2}{{a}^2}$, en donde, a es la longitud de uno de los lados del hexágono. Esto significa que el área de ambas caras hexagonales es $latex A=3\sqrt{3}{{a}^2}$.
El área de una de las caras rectangulares del prisma es igual a $latex ah$, en donde, a es la longitud de uno de los lados del hexágono y h es la altura del prisma. Entonces, el área de las seis caras rectangulares es igual a $latex 6ah$.
Al sumar las expresiones obtenidas para las áreas, tenemos:
| $latex A_{S}=3\sqrt{3}{{a}^2}+6ah$ |

Ejercicios de área y volumen de prismas hexagonales resueltos
EJERCICIO 1
¿Cuál es el volumen de un prisma hexagonal que tiene lados de longitud 4 m y una altura de 6 m?
Solución
Tenemos los siguientes datos:
- Lados del hexágono, $latex a=4$
- Altura, $latex h=6$
Usando la fórmula del volumen, tenemos:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(4)}^2}(6)$
$latex V=\frac{3\sqrt{3}}{2}(16)(6)$
$latex V=249.4$
El volumen es 249.4 m³.
EJERCICIO 2
¿Cuál es el área superficial de un prisma hexagonal que tiene una base hexagonal con lados de longitud 4 m y una altura de 6 m?
Solución
Tenemos los siguientes datos:
- Lados hexágono, $latex a=4$
- Altura prisma, $latex h=6$
Usando la fórmula del área superficial con estos valores, tenemos:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex A_{S}=3\sqrt{3}{{(4)}^2}+6(4)(6)$
$latex A_{S}=3\sqrt{3}(16)+144$
$latex A_{S}=83.14+90$
$latex A_{S}=173.14$
El área superficial es 173.14 m².
EJERCICIO 3
Un prisma hexagonal tiene lados de longitud 5 m y una altura de 5 m. ¿Cuál es su volumen?
Solución
De la pregunta, tenemos los siguientes datos:
- Lados del hexágono, $latex a=5$
- Altura, $latex h=5$
Reemplazando a estos valores en la fórmula del volumen, tenemos:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(5)}^2}(5)$
$latex V=\frac{3\sqrt{3}}{2}(16)(6)$
$latex V=324.8$
El volumen es 324.8 m³.
EJERCICIO 4
Tenemos un prisma con una altura de 10 m y una base hexagonal de lados con longitud de 5 m. ¿Cuál es su área superficial?
Solución
Reconocemos lo siguiente:
- Lados hexágono, $latex a=5$
- Altura prisma, $latex h=10$
Al usar la fórmula del área superficial con estos valores, tenemos:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex A_{S}=3\sqrt{3}{{(5)}^2}+6(5)(10)$
$latex A_{S}=3\sqrt{3}(25)+300$
$latex A_{S}=129.9+300$
$latex A_{S}=429.9$
El área superficial es 429.9 m².
EJERCICIO 5
¿Cuál es el volumen de un prisma hexagonal que tiene lados de longitud 7 m y una altura de 8 m?
Solución
Tenemos la siguiente información:
- Lados del hexágono, $latex a=7$
- Altura, $latex h=8$
Usamos a estos datos en la fórmula del volumen:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(7)}^2}(8)$
$latex V=\frac{3\sqrt{3}}{2}(49)(8)$
$latex V=1018.4$
El volumen es 1018.4 m³.
EJERCICIO 6
¿Cuál es la altura de un prisma que tiene un área superficial de 226.77 m² y una base hexagonal con lados de longitud 3 m?
Solución
Tenemos los siguientes datos:
- Lados hexágono, $latex a=3$
- Área superficial, $latex A=226.77$
En este caso, tenemos el área superficial y queremos encontrar la longitud de la altura del prisma. Entonces, usamos los valores dados en la fórmula y resolvemos para h:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex 226.77=3\sqrt{3}{{(3)}^2}+6(3)h$
$latex 226.77=46.77+18h$
$latex 18h=226.77-46.77$
$latex 18h=180$
$latex h=10$
La longitud de la altura es igual a 10 m.
EJERCICIO 7
Un prisma tiene una base hexagonal con lados de longitud 8 m y una altura de 9 m. ¿Cuál es su volumen?
Solución
Tenemos los siguientes datos:
- Lados del hexágono, $latex a=8$
- Altura, $latex h=9$
Usando la fórmula del volumen, tenemos:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(8)}^2}(9)$
$latex V=\frac{3\sqrt{3}}{2}(64)(9)$
$latex V=1496.5$
El volumen es 1496.5 m³.
EJERCICIO 8
Si es que un prisma tiene un área superficial de 542.6 m² y la base hexagonal tiene lados de longitud 6 m, ¿cuál es la longitud de su altura?
Solución
Tenemos lo siguiente:
- Lados hexágono, $latex a=6$
- Área superficial, $latex A=542.6$
Usamos la fórmula del área superficial con los valores dados y resolvemos para h:
$latex A_{S}=3\sqrt{3}{{a}^2}+6ah$
$latex 542.6=3\sqrt{3}{{(6)}^2}+6(6)h$
$latex 542.6=254.6+36h$
$latex 36h=542.6-254.6$
$latex 36h=288$
$latex h=8$
La longitud de la altura es igual a 8 m.
Ejercicios de área y volumen de prismas hexagonales para resolver


Si es que un prisma hexagonal tiene un área superficial de 475 m2 y su base tiene lados de longitud 6 m, ¿cuál es la longitud de su altura?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre prismas hexagonales? Mira estas páginas:


