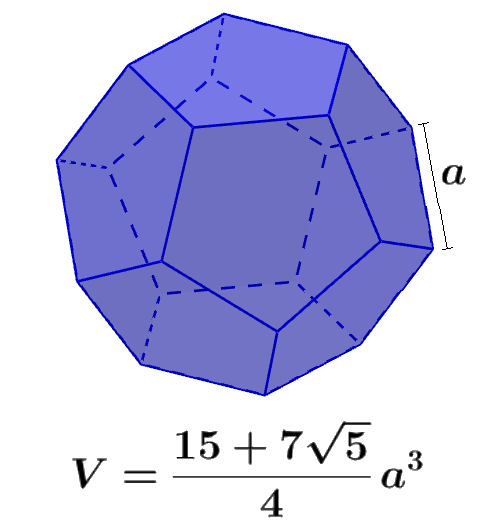
Los dodecaedros son uno de los cinco sólidos platónicos. Estas figuras son regulares, por lo que todas sus caras son iguales y tienen las mismas dimensiones. Entonces, podemos calcular su área superficial si multiplicamos el área de una cara por 12.
A continuación, conoceremos la fórmula del área superficial de un dodecaedro. Aprenderemos a derivar esta fórmula y la usaremos para resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial de un dodecaedro con ejercicios
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial de un dodecaedro con ejercicios
Fórmula del área superficial de un dodecaedro
Un dodecaedro se caracteriza por tener doce caras pentagonales congruentes. Es decir, las doce caras tienen las mismas dimensiones. Esta figura tridimensional es uno de los cinco sólidos platónicos.
Podemos calcular el área superficial de un dodecaedro usando la siguiente fórmula:
| $$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$ |
en donde, a es la longitud de uno de los lados del dodecaedro.
Podemos simplificar esta fórmula al aproximar la expresión en el lado derecho de la fórmula. Entonces, podemos escribir:
$latex A_{s}\approx 20.65{{a}^2}$
Derivación de la fórmula del área superficial de un dodecaedro
Para encontrar una fórmula para el área superficial de un dodecaedro, podemos considerar que los dodecaedros son figuras regulares que tienen 12 caras con la misma forma y las mismas dimensiones.
Dado que las 12 caras pentagonales del dodecaedro son las mismas, tenemos que encontrar el área de una de las caras y multiplicar el resultado por 12 para obtener el área superficial del dodecaedro.
Ahora, podemos encontrar el Área de un Pentágono usando la siguiente fórmula:
$$A=\frac{1}{4}\sqrt{25+10\sqrt{5}}~{{a}^2}$$
Entonces, cuando multiplicamos a esta fórmula por 12, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
Área superficial de un dodecaedro – Ejercicios resueltos
Los siguientes ejercicios son resueltos aplicando la fórmula del área superficial de un dodecaedro. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es el área superficial de un dodecaedro que tiene lados con una longitud de 1 m?
Solución
Para resolver este ejercicio, podemos aplicar la fórmula del área superficial de un dodecaedro con el valor a=1. Entonces, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{1}^2}$
$latex A_{s}=20.65$
El área superficial del dodecaedro es $latex 20.65~{{m}^2}$.
EJERCICIO 2
Determina el área superficial de un dodecaedro que tiene lados con una longitud de 2 m.
Solución
Usando la fórmula del área superficial con el valor a=2, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{2}^2}$
$latex A_{s}=20.65\times 4$
$latex A_{s}=82.6$
El área superficial del dodecaedro es $latex 82.6~{{m}^2}$.
EJERCICIO 3
Encuentra el área superficial de un dodecaedro que tiene lados con una longitud de 6 cm.
Solución
Aplicando la fórmula del área superficial usando a=6, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{6}^2}$
$latex A_{s}=20.65\times 36$
$latex A_{s}=743.4$
El área superficial del dodecaedro es $latex 743.4~{{cm}^2}$.
EJERCICIO 4
Si es que un dodecaedro tiene un área superficial de $latex 120~{{m}^2}$, ¿cuál es la longitud de sus lados?
Solución
En este problema, conocemos el área superficial y tenemos que determinar la longitud de uno de los lados del dodecaedro. Entonces, usamos la fórmula del área superficial y resolvemos para a:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex 120=20.65~{{a}^2}$
$latex 5.81=a^2$
$latex a=2.41$
El dodecaedro tiene lados con una longitud de 2.41 m.
EJERCICIO 5
¿Cuál es la longitud de los lados de un dodecaedro que tiene un área superficial de $latex 350~{{cm}^2}$?
Solución
Similar al problema anterior, vamos a usar la fórmula del área superficial y resolveremos para a. Entonces, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex 350=20.65~{{a}^2}$
$latex 16.95=a^2$
$latex a=4.12$
El dodecaedro tiene lados con una longitud de 4.12 cm.
EJERCICIO 6
Encuentra la longitud de los lados de un dodecaedro que tiene un área superficial de $latex 1300~{{cm}^2}$.
Solución
Usando la fórmula del área superficial y resolviendo para a, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex 1300=20.65~{{a}^2}$
$latex 62.95=a^2$
$latex a=7.93$
El dodecaedro tiene lados con una longitud de 7.93 cm.
EJERCICIO 7
¿Cuál es el área superficial de un dodecaedro que tiene lados con una longitud de 7 mm?
Solución
Usamos el valor a=7 en la fórmula del área superficial. Entonces, tenemos:
$$A_{s}=3\sqrt{25+10\sqrt{5}}~{{a}^2}$$
$latex A_{s}=20.65~{{a}^2}$
$latex A_{s}=20.65\times {{7}^2}$
$latex A_{s}=20.65\times 49$
$latex A_{s}=1011.85$
El área superficial del dodecaedro es $latex 1011.85~{{mm}^2}$.
Área superficial de un dodecaedro – Ejercicios para resolver
Resuelve los siguientes ejercicios aplicando la fórmula del área superficial de un dodecaedro. Selecciona una respuesta y haz clic en «Verificar» para comprobarla.
Véase también
¿Interesado en aprender más sobre dodecaedros? Echa un vistazo a estas páginas:
