El área de un rombo puede ser definida como la cantidad de espacio encerrada por un rombo en un espacio bidimensional. Recordemos que un rombo es un tipo de cuadrilátero proyectado en un plano de dos dimensiones (2D) que tiene cuatro lados que son iguales en longitud y son congruentes. También es conocido como un cuadrilátero equilátero, ya que sus cuatro lados son iguales.
A continuación, aprenderemos a calcular el área de un rombo. Conoceremos una fórmula que usa sus diagonales y otras fórmulas que usan sus lados. Además, resolveremos algunos ejercicios para aplicar las fórmulas.
¿Cómo se calcula el área de un rombo?
Para calcular el área de un rombo, podemos usar uno de los tres métodos principales que existen. Podemos usar sus diagonales, podemos usar su base y altura y podemos usar trigonometría.
Área del rombo usando diagonales: Método 1
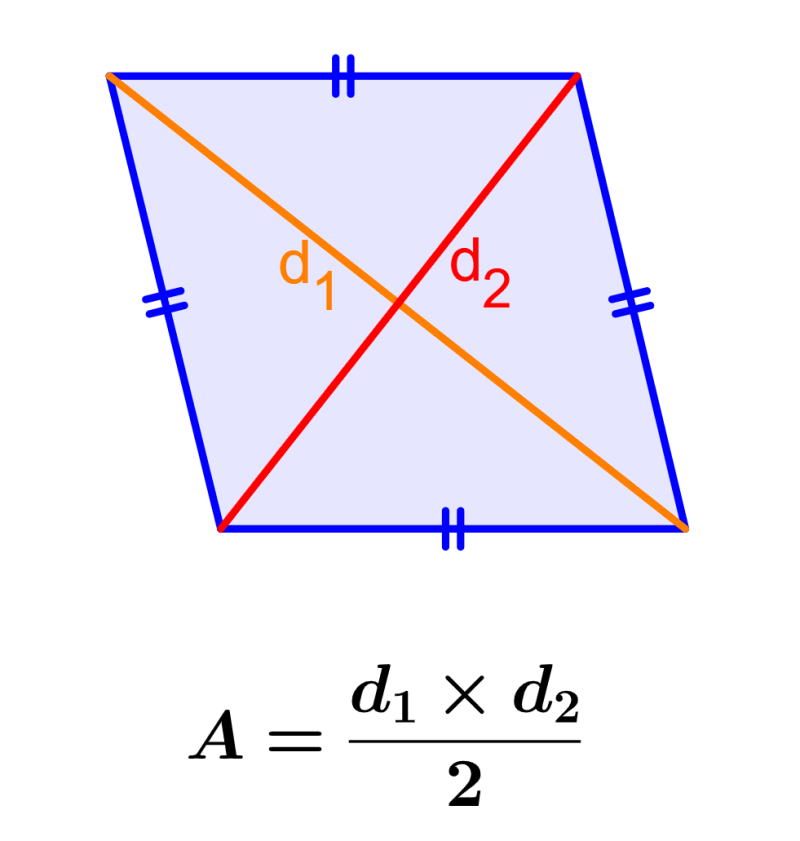
El área del rombo puede ser calculada usando la longitud de sus diagonales y la fórmula:
| $latex A=\frac{d_{1}\times d_{2}}{2}$ |
en donde,
- $latex d_{1}=$ longitud de la diagonal 1
- $latex d_{2}=$ longitud de la diagonal 2
- $latex A=$ área del rombo
Derivación de esta fórmula
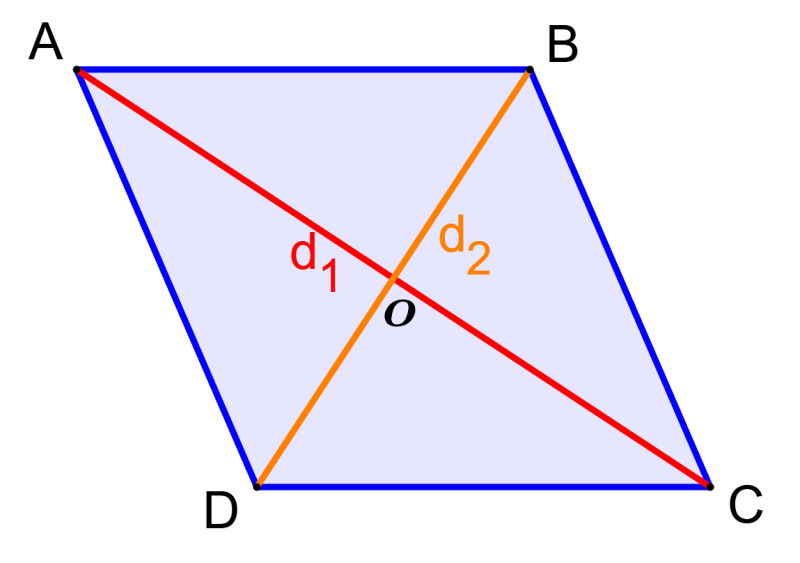
Considera al siguiente rombo:
Podemos representar con O al punto de intersección de las dos diagonales. Entonces, el área del rombo será:
$latex A=4\times\text{área de }\Delta AOB$
$latex =4\times(\frac{1}{2})\times AO \times OB$
$latex =4\times(\frac{1}{2})\times(\frac{1}{2})d_{1}\times(\frac{1}{2})d_{2}$
$latex =4\times(\frac{1}{8})d_{1}d_{2}$
$latex =\frac{1}{2}d_{1}d_{2}$
Entonces, el área de un rombo es $latex A=\frac{1}{2}d_{1}d_{2}$, en donde, $latex d_{1}$ y $latex d_{2}$ son las diagonales de un rombo.
Entonces, considerando a un rombo ABCD que tiene dos diagonales, por ejemplo, AC y BD, podemos usar los siguientes pasos para calcular su área:
Paso 1: Encuentra la longitud de la diagonal 1, $latex d_{1}$. Las diagonales de un rombo son perpendiculares la una a la otra formando cuatro ángulos rectos cuando se intersecan.
Paso 2: Encuentra la longitud de la diagonal 2, $latex d_{2}$.
Paso 3: Multiplica ambas diagonales, $latex d_{1}$ y $latex d_{2}$.
Paso 4: Divide el resultado por 2.
EJEMPLO 1
- Calcula el área de un rombo que tiene diagonales iguales a 8 cm y 10 cm.
Solución: Tenemos la siguiente información:
- Diagonal 1, $latex d_{1}=8$ cm
- Diagonal 2, $latex d_{2}=10$ cm
Usamos la fórmula del área del rombo con la información dada:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{8\times 10}{2}$
$latex =\frac{80}{2}$
$latex A=40$
Entonces, el área del rombo es 40 cm².
EJEMPLO 2
- ¿Cuál es el área de un rombo que tiene diagonales iguales a 10 m y 12 m?
Solución: Tenemos los siguientes valores:
- Diagonal 1, $latex d_{1}=10$ m
- Diagonal 2, $latex d_{2}=12$ m
Reemplazando estos valores en la fórmula, tenemos:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{10\times 12}{2}$
$latex =\frac{120}{2}$
$latex A=60$
Entonces, el área del rombo es 60 m².
Resuelve los siguientes ejercicios
¿Cómo calcular el área de un rombo sin diagonales?
El área de un rombo también puede ser calculada sin las diagonales. Tenemos dos métodos para realizar esto.
Área del rombo usando la base y la altura: Método 2
El área del rombo puede ser calculada usando la base y la altura con la fórmula:
| $latex A=bh$ |
en donde,
- $latex b=$ longitud de cualquier lado del rombo
- $latex h=$ longitud de la altura del rombo
- $latex A=$ área del rombo
Entonces, calculamos el área del rombo a partir de su base y altura con los siguientes pasos:
Paso 1: Encuentra la altura y la base del rombo. La base del rombo es uno de sus lados y la altura es la distancia perpendicular desde la base escogida hasta el lado opuesto.
Paso 2: Multiplica la base y la altura obtenida.
EJEMPLO
- ¿Cuál es el área de un rombo que tiene una base de 8 m y una altura de 6 m?
Solución: Tenemos los siguientes valores:
- Base, $latex b=8$ m
- Altura, $latex h=6$ m
Usando estos valores con la fórmula, tenemos:
$latex A=bh$
$latex =(8)(6)$
$latex A=48$
Entonces, el área del rombo es 48 m².
Resuelve el siguiente ejercicio
Área del rombo usando trigonometría: Método 3
Podemos calcular el área de un rombo usando trigonometría con la siguiente fórmula:
| $latex A={{b}^2}\times \sin(a)$ |
en donde,
- $latex b=$ longitud de cualquier lado del rombo
- $latex a=$ medida de cualquier ángulo interno
- $latex A=$ área del rombo
Entonces, podemos usar los siguientes pasos para calcular el área de un rombo usando trigonometría:
Paso 1: Eleva al cuadrado la longitud de cualquier de los lados del rombo.
Paso 2: Multiplica el resultado del paso 1 por el seno de uno de sus ángulos.
EJEMPLO
- Un rombo tiene lados de longitud 10 m y un ángulo interno mide 60°. ¿Cuál es su área?
Solución: Tenemos los siguientes datos:
- Lado, $latex b=10$ m
- Ángulo, $latex a=60°$
Usando esta información en la fórmula, tenemos:
$latex A={{b}^2}\times \sin(60°)$
$latex ={{10}^2}\times 0.866$
$latex =100\times 0.866$
$latex A=866$
Entonces, el área del rombo es 866 m².
Resuelve el siguiente ejercicio
Véase también
¿Interesado en aprender más sobre rombos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
