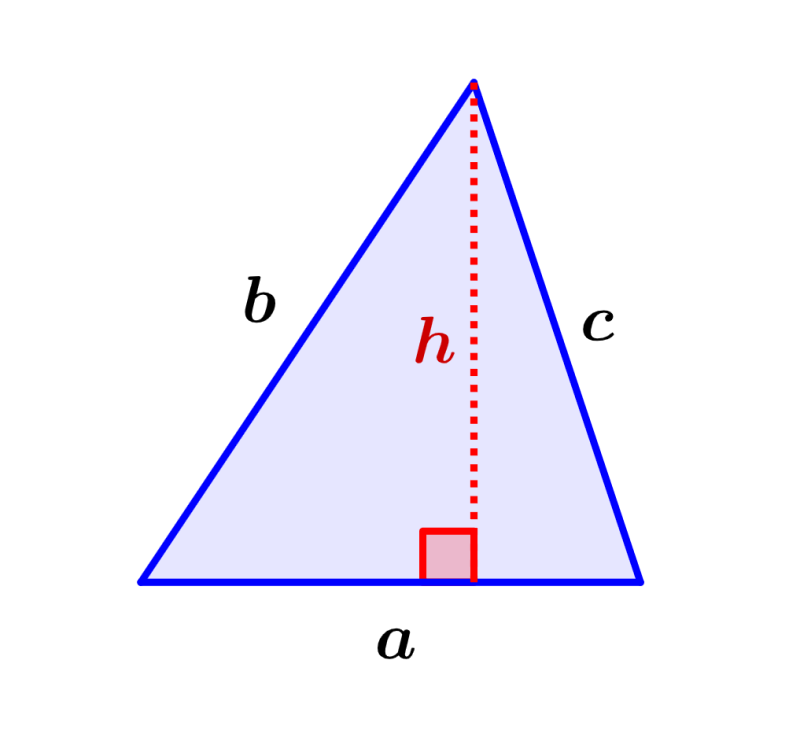
La altura de un triángulo es la distancia perpendicular desde la base hasta el vértice opuesto. Podemos calcular la altura de un triángulo escaleno usando fórmulas diferentes dependiendo en la información que tengamos disponible. Por ejemplo, podemos calcular la altura si es que conocemos las longitudes de todos los lados. Adicionalmente, podemos usar la longitud de un lado y un ángulo adyacente o también, podemos usar el área y la longitud de la base.
A continuación, conoceremos las diferentes fórmulas que podemos usar para encontrar la altura de un triángulo escaleno. Además, veremos algunos ejercicios en los que aplicaremos estas fórmulas para obtener la respuesta.
GEOMETRÍA
Relevante para…
Aprender sobre la altura de un triángulo escaleno con ejercicios.
GEOMETRÍA
Relevante para…
Aprender sobre la altura de un triángulo escaleno con ejercicios.
Fórmula de la altura de un triángulo escaleno
Dependiendo en la información que tengamos disponible, podemos usar dos fórmulas diferentes para encontrar la altura de un triángulo escaleno.
Altura de un triángulo escaleno si es que conocemos todos sus lados
Cuando conocemos las longitudes de todos los lados del triángulo, podemos calcular la altura usando una fórmula que es derivada de la fórmula de Herón, la cual es usada para calcular el área:
| $latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$ |
en donde,
- $latex a, ~b, ~c$ son las longitudes de los lados del triángulo
- $latex S$ es el semiperímetro, el cual es igual a $latex S=\frac{a+b+c}{2}$
- $latex h$ es la altura perpendicular a la base
Altura de un triángulo escaleno si es que conocemos un lado y su ángulo o el área y su base
Si es que conocemos la longitud de uno de sus lados y la medida de uno de sus ángulos o si es que conocemos su área y la longitud de su base, podemos usar las siguientes fórmulas:
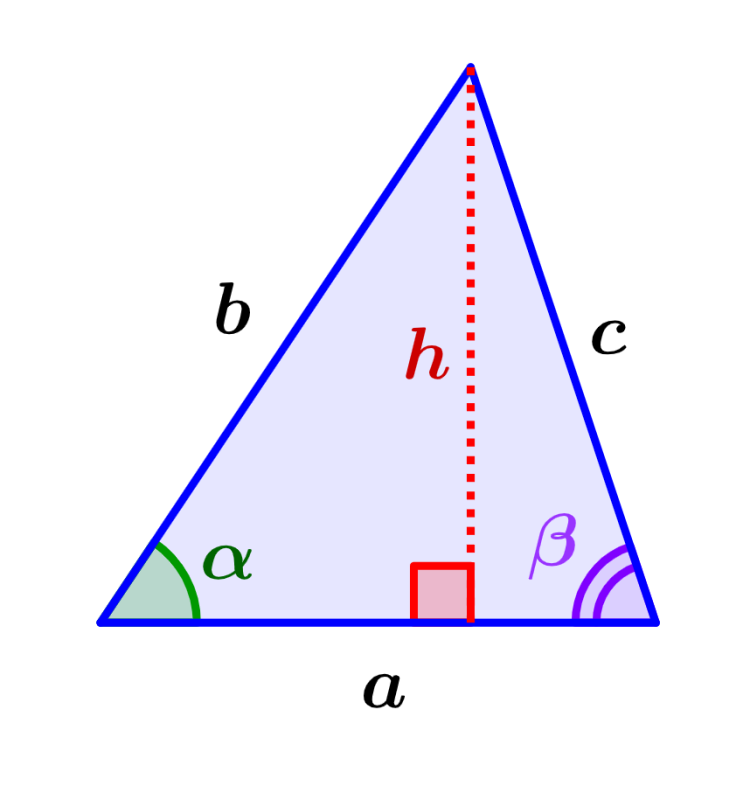
| $latex h=b\cdot\sin(\alpha)$ $latex h=c\cdot\sin(\beta)$ $latex h=\frac{2A}{a}$ |
en donde,
- $latex b,~c$ son las longitudes de los lados laterales
- $latex a$ es la longitud de la base
- $latex \alpha,~\beta$ son las medidas de los ángulos en la base
- $latex A$ es el área del triángulo
- $latex h$ es la altura perpendicular a la base
Ejercicios de altura de un triángulo escaleno resueltos
Las fórmulas de la altura de un triángulo escaleno indicadas arriba son aplicadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Un triángulo escaleno tiene lados de longitudes 6 m, 8 m y 10 m, en donde la base mide 6 m ¿Cuál es la longitud de su altura?
Solución
Podemos usar la primera fórmula con los siguientes datos:
- Lado 1 y base, $latex a=6$m
- Lado 2, $latex b=8$m
- Lado 3, $latex c=10$m
Reemplazamos estos valores en la fórmula:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
Para encontrar S, usamos la fórmula:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{6+8+10}{2}$
$latex S=\frac{24}{2}$
$latex S=12$
Usando estos valores, tenemos:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
$latex h=\frac{2}{6}\sqrt{12(12-6)(12-8)(12-10)}$
$latex h=\frac{2}{6}\sqrt{12(6)(4)(2)}$
$latex h=\frac{2}{6}\sqrt{576}$
$latex h=\frac{2}{6}(24)$
$latex h=8$
La altura es 8 m.
EJERCICIO 2
Un triángulo escaleno tiene lados de longitudes 12 m, 14 m y 16 m y la base es 14 m. ¿Cuál es la longitud de su altura?
Solución
Tenemos la siguiente información:
- Lado 1, $latex a=12$m
- Lado 2 y base, $latex b=14$m
- Lado 3, $latex c=16$m
Reemplazamos estos valores en la fórmula:
$latex h=\frac{2}{b}\sqrt{S(S-a)(S-b)(S-c)}$
Empezamos encontrando S:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{12+14+16}{2}$
$latex S=\frac{42}{2}$
$latex S=21$
Al usar estos valores, tenemos:
$latex h=\frac{2}{a}\sqrt{S(S-a)(S-b)(S-c)}$
$latex h=\frac{2}{14}\sqrt{21(21-12)(21-14)(21-16)}$
$latex h=\frac{2}{14}\sqrt{21(9)(7)(5)}$
$latex h=\frac{2}{14}\sqrt{6615}$
$latex h=\frac{2}{14}(81.33)$
$latex h=11.62$
La altura es 11.62 m.
EJERCICIO 3
¿Cuál es la longitud de la altura de un triángulo si es que un lado lateral mide 16 m y su ángulo en la base mide 30°?
Solución
Podemos usar la siguiente fórmula:
$latex h=b\cdot \sin(\alpha)$
en donde, $latex b=16$ m y $latex \alpha=30$°. Entonces, tenemos:
$latex h=b\cdot \sin(\alpha)$
$latex h=16\cdot \sin(30)$
$latex h=16(0.5)$
$latex h=8$
La longitud de la altura es 8 m.
EJERCICIO 4
¿Cuál es la longitud de la altura de un triángulo si es que un lado lateral mide 22 m y su ángulo en la base mide 60°?
Solución
Usamos la siguiente fórmula:
$latex h=b\cdot \sin(\alpha)$
en donde, $latex b=22$ m y $latex \alpha=60$°. Entonces, tenemos:
$latex h=b\cdot \sin(\alpha)$
$latex h=22\cdot \sin(60)$
$latex h=22(0.866)$
$latex h=19.05$
La longitud de la altura es 19.05 m.
EJERCICIO 5
¿Cuál es la altura de un triángulo escaleno que tiene un área de 100 m² y una base de 25 m?
Solución
Podemos usar la fórmula:
$latex h= \frac{2A}{b}$
en donde, $latex b=25$ m y $latex A=100$ m². Entonces, tenemos:
$latex h= \frac{2A}{b}$
$latex h= \frac{2(100)}{25}$
$latex h= 8$
La altura es 8 m.
Ejercicios de altura de un triángulo escaleno para resolver
Usa las fórmulas de la altura de un triángulo escaleno para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre triángulos escalenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
