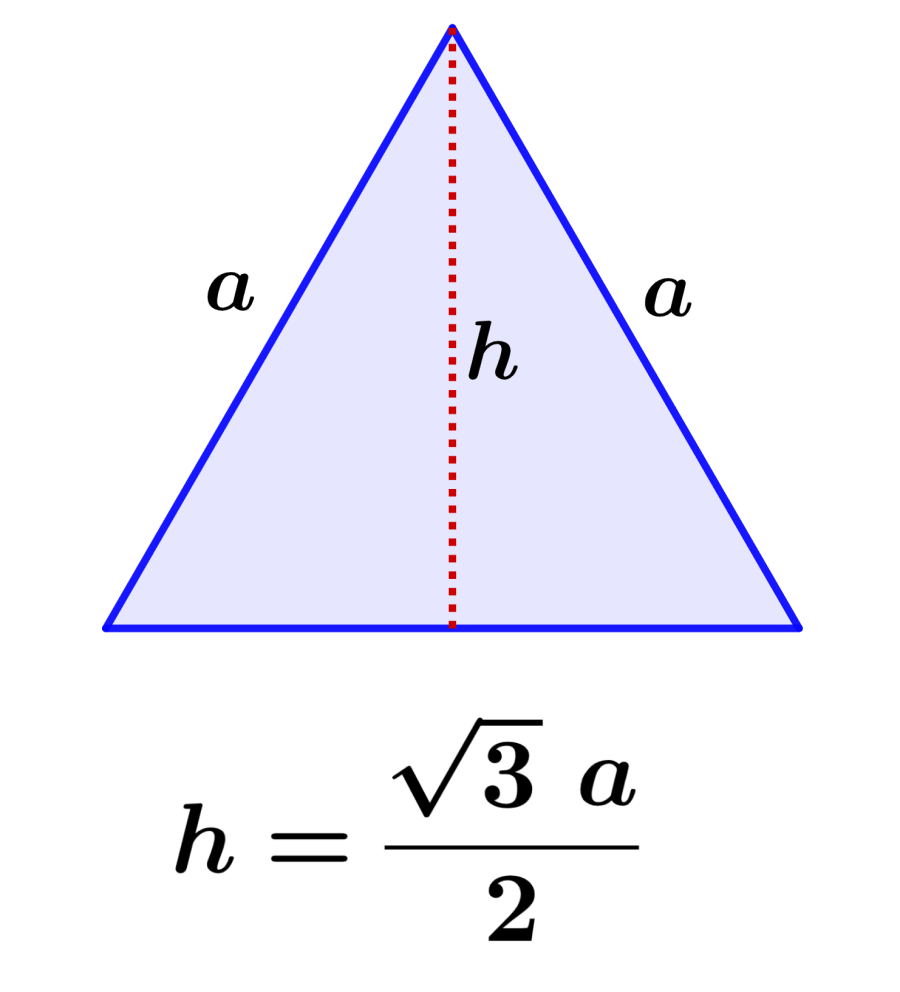
La altura de un triángulo equilátero es el segmento de línea que une al vértice con su lado opuesto. La altura es la mediatriz del lado opuesto al vértice y divide al triángulo en dos triángulos iguales con ángulos rectos. Podemos encontrar una fórmula para la altura del triángulo equilátero usando el teorema de Pitágoras.
A continuación, conoceremos todo lo relacionado con la altura de un triángulo equilátero. Aprenderemos cómo derivar su fórmula y la aplicaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a encontrar la altura de un triángulo equilátero con ejercicios.
GEOMETRÍA
Relevante para…
Aprender a encontrar la altura de un triángulo equilátero con ejercicios.
Fórmula de la altura de un triángulo equilátero
Los triángulos equiláteros son triángulos que tienen todos sus lados con la misma longitud. Podemos calcular la longitud de la altura de triángulos equiláteros usando la siguiente fórmula:
| $$h=\frac{\sqrt{3}~a}{2}$$ |
en donde, a es la longitud de uno de los lados del triángulo equilátero. Entonces, para determinar la altura de un triángulo equilátero, solo tenemos que conocer la longitud de uno de sus lados.
Demostración de la fórmula de la altura de un triángulo equilátero
Podemos demostrar la fórmula de la altura de un triángulo equilátero usando el teorema de Pitágoras. Recordemos que el teorema de Pitágoras nos dice que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa:
Hipotenusa2 = lado12+lado22
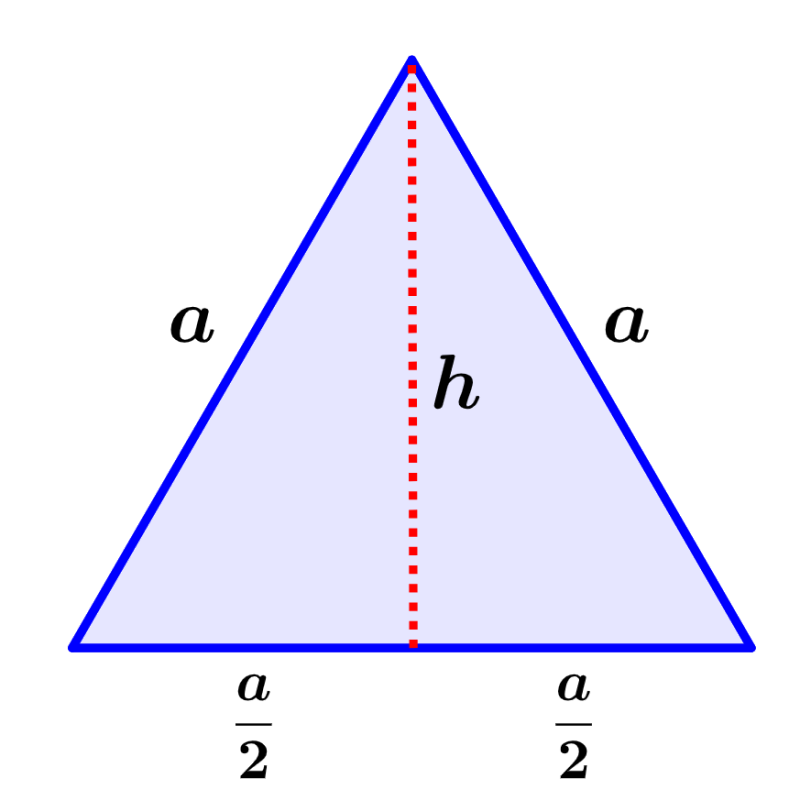
Ahora, podemos usar la siguiente figura:
En este triángulo, los lados tienen una longitud de a y la altura tiene una longitud de h. Podemos ver que la altura divide al triángulo en dos triángulos rectángulos iguales.
Podemos usar uno de los triángulos rectángulos para aplicar el teorema de Pitágoras. En cada triángulo, la hipotenusa es igual a a, la base es igual a a/2 y la altura es igual a h. Entonces, tenemos:
Hipotenusa2 = lado12+lado22
$$a^2 = h^2+ \left(\frac{a}{2}\right)^2$$
Ahora, solo tenemos que resolver esta ecuación para la altura h:
$$a^2 = h^2+ \left(\frac{a}{2}\right)^2$$
$$ h^2=a^2- \left(\frac{a^2}{4}\right)$$
$$ h^2= \frac{3a^2}{4}$$
$$ h= \frac{\sqrt{3}a}{2}$$
Entonces, hemos demostrado la fórmula de la altura de un triángulo equilátero.
Calcular la altura de un triángulo equilátero con el perímetro
Para encontrar la altura de un triángulo equilátero usando el perímetro, tenemos que empezar determinando la longitud de uno de los lados del triángulo.
Sabemos que los triángulos equiláteros tienen todos sus lados con la misma longitud. Entonces, simplemente podemos dividir al perímetro por 3 para encontrar la longitud de un lado.
Finalmente, aplicamos la fórmula de la altura de un triángulo equilátero usando la longitud hallada.
Alternativamente, podemos modificar la fórmula de la altura reemplazando p=3a o a=p/3, en donde p es el perímetro y a es la longitud de uno de los lados del triángulo. Entonces, tenemos:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}\frac{p}{3}}{2}$$
$$ h= \frac{\sqrt{3}p}{6}$$
Calcular la altura de un triángulo equilátero con el área
Para calcular la altura de un triángulo equilátero con el área, tenemos que usar la fórmula del área de un triángulo equilátero para determinar la longitud de uno de sus lados.
Recordemos que la fórmula del Área de un Triángulo Equilátero es:
$$ A= \frac{\sqrt{3}}{4}~a^2$$
Luego de encontrar la longitud de uno de los lados, podemos simplemente aplicar la fórmula de la altura.
Altura de un triángulo equilátero – Ejemplos resueltos
Los siguientes ejercicios son resueltos usando la fórmula de la altura de un triángulo equilátero. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra la longitud de la altura de un triángulo equilátero que tiene lados con una longitud de 2 m.
Solución
Vamos a usar la fórmula de la altura para encontrar la longitud que queremos. Sustituyendo el valor a=2, tenemos:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(2)}{2}$$
$latex h= \sqrt{3}$
La longitud de la altura del triángulo dado es $latex \sqrt{3}$.
EJERCICIO 2
¿Cuál es la altura de un triángulo equilátero que tiene lados de 5 cm?
Solución
Usando la fórmula de la altura con el valor a=5, tenemos:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(5)}{2}$$
$latex h= 4.33$
El triángulo equilátero tiene una altura que mide 4.33 cm.
EJERCICIO 3
Si es que la altura de un triángulo equilátero mide 6 cm, ¿cuál es la longitud de uno de sus lados?
Solución
En este caso, tenemos la longitud de la altura y queremos encontrar la longitud de uno de los lados del triángulo. Entonces, usamos la fórmula de la altura y resolvemos para a:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ 6= \frac{\sqrt{3}a}{2}$$
$latex 12= \sqrt{3}a$
$latex a=6.928$
La longitud de uno de los lados del triángulo es 6.928 cm.
EJERCICIO 4
Determina la longitud de los lados de un triángulo equilátero que tiene una altura de 8 m.
Solución
Similar al problema anterior, podemos usar la fórmula de la altura y resolver para a:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ 8= \frac{\sqrt{3}a}{2}$$
$latex 16= \sqrt{3}a$
$latex a=9.238$
El triángulo tiene lados con una longitud de 9.238 m.
EJERCICIO 5
El perímetro de un triángulo equilátero es igual a 30 cm. Encuentra la longitud de su altura.
Solución
El perímetro es la suma de las longitudes de los tres lados del triángulo. En un triángulo equilátero, los tres lados tienen la misma longitud, por lo que podemos dividir al perímetro por 3 para encontrar la longitud de uno de sus lados.
Entonces, sabemos que la longitud de uno de los lados del triángulo es 30/3=10. Ahora, podemos usar esa longitud en la fórmula de la altura y tenemos:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(10)}{2}$$
$latex h= 8.66$
La altura del triángulo mide 8.66 cm.
EJERCICIO 6
Determina la longitud de la altura de un triángulo equilátero que tiene un perímetro de 21 cm.
Solución
Similar al problema anterior, podemos encontrar la longitud de uno de los lados del triángulo equilátero si es que dividimos a su perímetro por 3.
Entonces, los lados del triángulo tienen una longitud de 18/3=6. Usando este valor en la fórmula de la altura, tenemos:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(6)}{2}$$
$latex h= 5.196$
La altura del triángulo mide 5.196 cm.
EJERCICIO 7
Si es que el área de un triángulo equilátero es igual a 60 cm2, ¿cuál es la longitud de su altura?
Solución
Para encontrar la longitud de la altura, tenemos que empezar encontrando la longitud de uno de los lados del triángulo. Para esto, podemos usar la fórmula del área de un triángulo equilátero con el valor dado y resolver para a:
$$ A= \frac{\sqrt{3}}{4}~a^2$$
$$ 60= \frac{\sqrt{3}}{4}~a^2$$
$latex a^2= 138.564$
$latex a= 11.77$
Ahora, usamos esta longitud encontrada en la fórmula de la altura:
$$ h= \frac{\sqrt{3}a}{2}$$
$$ h= \frac{\sqrt{3}(11.77)}{2}$$
$$ h= 10.193$$
La altura del triángulo mide 10.193 cm.
Altura de un triángulo equilátero – Ejercicios para resolver
Usa todo lo aprendido sobre la altura de un triángulo equilátero para resolver los siguientes ejercicios. Selecciona tu respuesta y haz clic en «Verificar» para conocer si es la solución correcta.
Véase también
¿Interesado en aprender más sobre triángulos equiláteros? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
