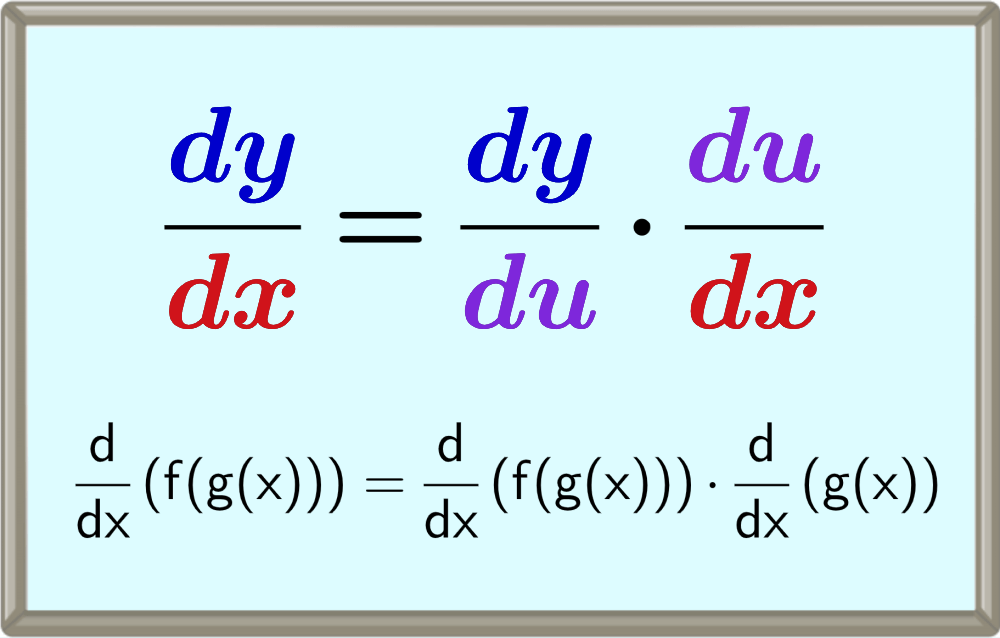Los problemas de derivación que involucran la composición de funciones se pueden resolver usando la fórmula de la regla de la cadena. Esta fórmula nos permite derivar una composición de funciones como f(g(x)).
Aquí, veremos un resumen de la regla de la cadena de derivadas. Además, exploraremos varios ejercicios con respuestas para comprender la aplicación de la fórmula de la regla de la cadena.
Resumen de la regla de la cadena
La regla de la cadena es una herramienta muy útil que se utiliza para derivar una composición de diferentes funciones. Es una regla que establece que la derivada de una composición de al menos dos tipos diferentes de funciones es igual a la derivada de la función exterior f(u) multiplicada por la derivada de la función interior g(x), donde u=g(x).
Esto nos da la fórmula de la regla de la cadena como:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{x}(g(x))$$
o en otra forma, se puede ilustrar como:
$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$
en donde
- $latex f(u) =$ la función exterior
- $latex u = g(x)$, el dominio de la función externa $latex f(u)$
- $latex \frac{dy}{du} =$ la derivada de la función exterior $latex f(u)$ en términos de $latex u$
- $latex \frac{du}{dx} =$ la derivada de la función interna $latex g(x)$ en términos de $latex x$
Usamos esta fórmula para derivar funciones que tienen las siguientes formas:
$latex H(x) = f(g(x))$
Regla de la cadena de derivadas – Ejercicios resueltos
EJERCICIO 1
Deriva la siguiente función:
$latex H(x) = (x+2)^2$
Solución
Lo primero que debemos hacer es escribir la fórmula de la regla de la cadena para nuestra referencia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{x}(g(x))$$
Suponiendo que eres un principiante, identifiquemos las funciones involucradas a partir de la composición de funciones:
Tenemos
$latex H(x) = (x+2)^2$
Si es que usamos la sustitución $latex u = g(x) = x+2$, podemos escribir
$latex f(g(x)) = f(u)$
$latex f(u) = u^2$
Aplicando la fórmula de la regla de la cadena tenemos:
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^2) \cdot \frac{d}{x}(x+2)$$
$$\frac{d}{dx} (H(x)) = (2u) \cdot (1)$$
Dado que $latex u = x+2$, sustituyamos de vuelta:
$$\frac{d}{dx} (H(x)) = [2 \cdot (x+2)] \cdot (1)$$
Simplificando algebraicamente, tenemos
$latex H'(x) = 2(x+2)$
Y la respuesta final es:
$latex H'(x) = 2x + 4$
EJERCICIO 2
Encuentra la derivada de
$latex H(x) = (x^3 – 3x^2 + 2x)^5$
Solución
Si es que usamos la sustitución $latex g(x) = u=x^3 – 3x^2 + 2x$, tenemos:
$latex f(g(x)) = f(u)$
$latex f(u) = u^5$
Aplicando la fórmula de la regla de la cadena tenemos:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^5) \cdot \frac{d}{dx}(x^3 – 3x^2 + 2x)$$
$$\frac{d}{dx} (H(x)) = (5u^4) \cdot (3x^2-6x+2)$$
Ahora, podemos sustituir $latex u=x^3 – 3x^2 + 2x$ de vuelta:
$$\frac{d}{dx} (H(x)) = [5 \cdot (x^3 – 3x^2 + 2x)^4]\cdot (3x^2-6x+2)$$
Simplificando algebraicamente, tenemos
$$H'(x) = (5x^3-15x^2+10x)^4 \cdot (3x^2-6x+2)$$
Y la respuesta final es:
$$H'(x) = (5x^3-15x^2+10x)^4 (3x^2-6x+2)$$
EJERCICIO 3
Deriva la siguiente función:
$latex F(x) = \ln{(3x^2-1)}$
Solución
Si es que consideramos $latex g(x)=u=3x^2-1$, podemos escribir de la siguiente forma:
$latex f(g(x)) = f(u)$
$latex f(u) = \ln{(u)}$
Entonces, aplicamos la regla de la cadena:
$$ \frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{x}(g(x))$$
$$\frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$
$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\ln(u)) \cdot \frac{d}{x}(3x^2-1)$$
$$\frac{d}{dx} (F(x)) = (\frac{1}{u}) \cdot (6x)$$
Sustituyendo $latex u=3x^2-1$ de vuelta, tenemos:
$$\frac{d}{dx} (F(x)) = (\frac{1}{3x^2-1}) \cdot (6x)$$
Simplificando, tenemos
$$F'(x) = \frac{6x}{3x^2-1}$$
Y la respuesta final es:
$$F'(x) = \frac{6x}{3x^2-1}$$
EJERCICIO 4
¿Cuál es la derivada de la siguiente función?
$latex G(x) = e^{3x^2+1}$
Solución
Empezamos considerando que la función interna es $latex g(x)=u=3x^2+1$. Entonces, la composición de funciones puede ser escrita como:
$latex f(g(x)) = f(u)$
$latex f(u) = e^u$
Aplicando la fórmula de la regla de la cadena, tenemos:
$$\frac{d}{dx} (G(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{x}(g(x))$$
$$\frac{d}{dx} (G(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$
$$\frac{d}{dx} (G(x)) = \frac{d}{du} (e^u) \cdot \frac{d}{x}(3x^2+1)$$
$$\frac{d}{dx} (G(x)) = (e^u) \cdot (6x)$$
Dado que $latex u = 3x^2+1$, sustituyamos en la derivada:
$$\frac{d}{dx} (G(x)) = (e^{3x^2+1}) \cdot (6x)$$
$$G'(x) = 6x \cdot e^{3x^2+1}$$
Y la respuesta final es:
$$G'(x) = 6xe^{3x^2+1}$$
EJERCICIO 5
Usa la regla de la cadena para derivar la siguiente función:
$latex H(x) = \cos{(x^3-9)}$
Solución
Si es que consideramos a la función interna como $latex g(x) = u=x^3-9$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = \cos(u)$
Aplicando la fórmula de la regla de la cadena, tenemos:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (\cos(u)) \cdot \frac{d}{dx}(x^3 – 9)$$
$$\frac{d}{dx} (H(x)) = (-\sin(u)) \cdot (3x^2)$$
Dado que $latex u = g(x)$, sustituyamos $latex g(x)$ en $latex u$:
$$\frac{d}{dx} (H(x)) = (-\sin(x^3-9)) \cdot (3x^2)$$
Simplificando, tenemos
$latex H'(x) = -3x^2 \cdot \sin{(x^3-9)}$
Y la respuesta final es:
$latex H'(x) = -3x^2 \sin{(x^3-9)}$
EJERCICIO 6
Encuentra la derivada de
$latex H(x) = \sqrt[3]{x^3 – 3x^2 + 2x}$
Solución
Identifiquemos las funciones involucradas a partir de la composición de funciones:
Tenemos
$$H(x) = \sqrt[3]{x^3 – 3x^2 + 2x}$$
Dado que esta es una función radical, siempre se recomienda reescribirla de forma radical a exponente para que sea derivable. Reescribiendo, tenemos
$$ H(x) = (x^3 – 3x^2 + 2x)^{\frac{1}{3}}$$
Si es que $latex g(x) = u=x^3-3x^2+2x$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = u^{\frac{1}{3}}$
Al usar la regla de la cadena con estas funciones, tenemos:
$$ \frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$
$$ \frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^{\frac{1}{3}} ) \cdot \frac{d}{dx}(x^3 – 3x^2 + 2x)$$
$$\frac{d}{dx} (H(x)) = (\frac{1}{3} u^{-\frac{2}{3}}) \cdot (3x^2-6x+2)$$
Ahora, podemos sustituir $latex u=g(x)$ de vuelta:
$$\frac{d}{dx} (H(x)) = [(\frac{1}{3} \cdot (x^3 – 3x^2 + 2x)^{-\frac{2}{3}})]\cdot (3x^2-6x+2)$$
Simplificando, tenemos
$$H'(x) = \frac{1}{3 \cdot (x^3 – 3x^2 + 2x)^{\frac{2}{3}}} \cdot (3x^2-6x+2)$$
$$H'(x) = \frac{3x^2-6x+2}{3 \cdot (x^3 – 3x^2 + 2x)^{\frac{2}{3}}}$$
Y la respuesta final es:
$$H'(x) = \frac{3x^2-6x+2}{3 \sqrt[3]{(x^3 – 3x^2 + 2x)^2}}$$
en forma radical
EJERCICIO 7
Calcula la derivada de la función
$latex H(x)=\sec^{5}{x}$
Solución
Considerando a $latex g(x) = u=\sec(x)$ como la función interna, podemos escribir
$latex f(g(x)) = f(u)$
$latex f(u) = u^5$
Al usar la regla de la cadena, tenemos:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^5 ) \cdot \frac{d}{dx}(\sec{(x)})$$
$$\frac{d}{dx} (H(x)) = (5u^4) \cdot (\sec{(x)} \tan{(x)})$$
Ahora, podemos sustituir $latex u=\sec(x)$ de vuelta en la derivada:
$$\frac{d}{dx} (H(x)) = [5(\sec(x))^4] \cdot (\sec(x) \tan(x))$$
Simplificando, tenemos
$$H'(x) = 5 \cdot \sec{(x)} \cdot \sec^{4}{(x)} \cdot \tan(x)$$
$$H'(x) = 5 \cdot \tan(x) \cdot \sec^{5}{(x)}$$
Y la respuesta final es:
$latex H'(x) = 5 \tan{(x)} \sec^{5}{(x)}$
EJERCICIO 8
Encuentra la derivada de la siguiente función
$latex F(x) = \log_{7}{(x^3+e^x)}$
Solución
Si es que $latex g(x) = u=x^3+e^x$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = \log_{7}{u}$
Aplicando la fórmula de la regla de la cadena tenemos:
$$\frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\log_{7}{u} ) \cdot \frac{d}{dx}(x^3+e^x)$$
$$\frac{d}{dx} (F(x)) = \left(\frac{1}{u \ln(7)} \right) \cdot (3x^2+e^x)$$
Ahora, vamos a sustituir $latex u=x^3+e^x$:
$$\frac{d}{dx} (F(x)) = \left(\frac{1}{(x^3+e^x) \ln(7)} \right) \cdot (3x^2+e^x)$$
Simplificando algebraicamente, tenemos
$$\frac{d}{dx} (F(x)) = \left(\frac{1}{(x^3+e^x) \ln{(7)}} \right) \cdot (3x^2+e^x)$$
$$\frac{d}{dx} (F(x)) = \left(\frac{3x^2+e^x}{(x^3+e^x) \ln{(7)}} \right)$$
Y la respuesta final es:
$$F'(x) = \left(\frac{3x^2+e^x}{(x^3+e^x) \ln{(7)}} \right)$$
EJERCICIO 9
Usa la regla de la cadena para encontrar la derivada de
$$F(x) = \cot^{-1}{\left(\frac{x-1}{x+2} \right)}$$
Solución
Considerando a $latex g(x)=u=\frac{x-1}{x+2}$ como la función interna, tenemos:
$latex f(g(x)) = f(u)$
$latex f(u) = \cot^{-1}{(u)}$
Ahora, podemos usar la regla de la cadena con las funciones que hemos definido:
$$\frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$
$$ \frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\cot^{-1}(u)) \cdot \frac{d}{dx} \left(\frac{x-1}{x+2} \right)$$
$$\frac{d}{dx} (F(x)) = \left(-\frac{1}{u^2+1} \right) \cdot \left(\frac{2}{(x+1)^2} \right)$$
Dado que $latex u = g(x)$, sustituyamos $latex g(x)$ en $latex u$:
$$\frac{d}{dx} (F(x)) = \left(-\frac{1}{ \left(\frac{x-1}{x+1} \right)^2+1} \right) \cdot \left(\frac{2}{(x+1)^2} \right)$$
Simplificando, tenemos
$$\frac{d}{dx} (F(x)) = -\frac{2}{\left(\left(\frac{x-1}{x+1} \right)^2+1\right) \cdot (x+1)^2}$$
$$\frac{d}{dx} (F(x)) = -\frac{1}{x^2+1}$$
Y la respuesta final es:
$$F'(x) = -\frac{1}{x^2+1}$$
EJERCICIO 10
¿Cuál es la derivada de la siguiente función?
$latex f(x) = \tan^{2}{(e^{3x})}$
Solución
Este es un caso más complejo ya que la función $latex H(x)$ es una composición de cuatro funciones.
Si es que $latex f(g(h(j(x)))) = u$, entonces
$latex f(g(h(j(x)))) = f(u)$
$latex f(u) = u^2$
Si es que $latex g(h(j(x))) = v$, entonces
$latex g(h(j(x))) = g(v)$
$latex g(v) = \tan{(v)}$
Si es que $latex h(j(x)) = w$, entonces
$latex h(j(x)) = h(w)$
$latex h(w) = e^w$
$latex w = j(x) = 3x$
Si es que $latex f(g(h(j(x)))) = f(u)$, entonces
$$\frac{d}{dx} [f(g(h(j(x))))] = \frac{d}{du} [f(u)]$$
Si es que $latex g(h(j(x))) = g(v)$, entonces
$$\frac{d}{dx} [g(h(j(x)))] = \frac{d}{dv} [g(v)]$$
Si es que $latex h(j(x)) = h(w)$, entonces
$$\frac{d}{dx} [h(j(x))] = \frac{d}{dw} [h(w)]$$
Ajustando nuestra fórmula de la regla de la cadena para la derivada de composiciones de cuatro funciones, tenemos
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(h(j(x)))) \right)\cdot \frac{d}{dx} \left(g(h(j(x))) \right) \cdot \left(h(j(x)) \right) \cdot \frac{d}{dx}(j(x))$$
$$\frac{d}{dx} (H(x)) = \frac{d}{du} \left(f(u)) \right) \cdot \frac{d}{dv} \left(g(v)) \right) \cdot \frac{d}{dw} \left(h(w)) \right) \cdot \frac{d}{dx}(j(x))$$
Aplicando nuestra fórmula de la regla de la cadena ajustada para la derivada de la composición de cuatro funciones, tenemos
$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^2) \cdot \frac{d}{dv} (\tan{(v)}) \cdot \frac{d}{dw} (e^w) \cdot \frac{d}{dx}(3x)$$
$$\frac{d}{dx} (H(x)) = (2u) \cdot (\sec^{2}{(v)}) \cdot (e^w) \cdot (3)$$
Dado que $latex u = g(h(j(x)))$, $latex v = h(j(x))$ y $latex w = j(x)$, hagamos las sustituciones:
$$\frac{d}{dx} (H(x)) = (2(\tan{(e^{3x})})) \cdot (\sec^{2}{(e^{3x})}) \cdot (e^{3x}) \cdot (3)$$
Simplificando algebraicamente, tenemos
$$\frac{d}{dx} (H(x)) = 2 \cdot 3 \cdot e^{3x} \cdot \tan{(e^{3x})} \cdot \sec^{2}{(e^{3x})}$$
$$H'(x) = 6 \cdot (e^{3x}) \cdot \tan{(e^{3x})} \cdot \sec^{2}{(e^{3x})}$$
Y la respuesta final es:
$$ H'(x) = 6 \cdot (e^{3x}) \tan{(e^{3x})} \sec^{2}{(e^{3x})}$$
Como puede observar en nuestra solución a este problema, derivando composiciones de cuatro funciones, se dará cuenta de por qué la regla de la cadena se acuñó a partir del término «cadena».
Regla de la cadena de derivadas – Ejercicios para resolver
Encuentra la derivada de la siguiente función y determina el valor de $latex F^{\prime}(0)$: $latex F(x) = (x^3+\sin{(x)})^2$?
Escribe la respuesta en la casilla.
Veáse también
¿Interesado en aprender más sobre la regla de la cadena? Echa un vistazo a estas páginas: